Introduction
In recent years, a 12-pulse voltage-source converter based on high-voltage direct current (HVDC) transmission network has been widely implemented in real time, because of its outstanding advantages, such as economical efficiency and flexibility. Moreover, HVDC transmission systems that utilize the line-commutated converter (LCC) are successful and have been running for many years (
Wang and Sa-Nguyen et al. 2014;
Sanjeevikumar et al. 2014). However, on the point of safety, the operation of HVDC systems is essential for both monitoring and better protection. Many research articles have addressed various fault diagnostic postprocessing tools including artificial neural networks, fuzzy control, and other intelligent systems (
Nanayakkara 2011,
2012;
Mohagheghi et al. 2009). However, under high-power transmission conditions or produced complex strategies, they do not effectively find the fault that has actually occurred. Discrete wavelet transformation (DWT) has found wider applications recently for controlling the AC/DC drives and motors with major benefits and is discussed in detail by
Saleh (2013),
Hui et al. (2015),
Febin Daya et al. (2013a,
2013b,
2015,
2016), and
Sanjeevikumar et al. (2015a,
2015b,
2015c). Furthermore, wavelet transforms are applied in the field of HVDC transmission for diagnosis of fault location, analysis, and DC-link failure, but a systematic and comprehensive investigation of types of fault identification has not been presented (
De Kerf et al. 2011;
Yeap and Ukil 2014;
de Andrade and Ponce de Leao 2014) and moreover that is not robust to adaptations. DWT is the fast processing algorithm and its inherent capabilities are exploited as a fault diagnostic tool in this paper. A set of three drastic faulty conditions are developed for a 12-pulse LCC-HVDC transmission system as a preliminary investigation to verify the proposal—specifically, single-line-to-ground, on generation and on load end converters, and DC-link faults. The complete AC power system is numerically developed in the MATLAB/PLECS simulation software. The observed results presented in this paper show that DWT accurately predicts the types of developed fault conditions under all conditions, as expected.
Discrete wavelet transform for a 12-pulse LCC-HVDC power system
Figure 1 shows the schematic circuit of the standard 12-pulse LCC-HVDC transmission system in practice. The well-known synchronous reference frame regulation scheme is employed to control the 12-pulse rectifier and 12-pulse inverter units to perform effectively in the available power transfer from generation to the load center (
Sanjeevikumar et al. 2014). A set of three fault conditions are designed as a preliminary task to examine the most common and drastic issues in transmission networks—single-line-to-ground, on generation and on the load side converters, and most important DC-link faults. Furthermore, the research work is kept under study for investigation of types of fault identification and its detailed analysis as near future implementations.
In this analysis, the DWT plays the role of identifying about the set of faults under test and confirms the type of occurrences in the complete system. The input parameter is chosen as power, as it includes the characteristic variation in voltages and currents and adheres to be a simplified solution. The instantaneous power is calculated and fed as input to DWT, which begins processing when a discrete signal
x[
n] of length
N is transmitted. DWT can easily distinguish between the instantaneous power into high-pass signal resulting in an impulse response
h[
n] and that into a low-pass signal resulting in an impulse
g[
n], mathematically expressed as follows (
Saleh 2013;
Hui et al. 2015;
Febin Daya et al. 2013a,
2013b,
2015,
2016;
Sanjeevikumar et al. 2015a,
2015b,
2015c;
Mallat 1989):
where
d 1[
n] and
a 1[
n] are the outputs of the high- and low-pass filters, respectively. After this processing, again the output from the low-pass filter is down-sampled by two and passed through a low- and a high-pass filter, which resembles the ones in the first level, written as follows (second level of decomposition):
To be noted, several types of wavelet filters are available and have been investigated, but the minimum description length (MDL) is chosen as the best criterion and is mathematically represented as follows (
Febin Daya et al. 2013a,
2013b,
2015,
2016;
Sanjeevikumar et al. 2015a,
2015b,
2015c;
Mallat 1989):
where
denotes a vector of the wavelet transformed coefficients of the signal
f using wavelet filters (
n).
denotes a vector that contains
k nonzero elements. The threshold parameter
∅ K keeps
k number of the largest elements of the vector
constant and sets all other elements to zero.
N and
M denote the length of the signal and the number of wavelet filters, respectively. The entropy
H(
x) of a signal
x[
n] of length
N is defined by
For determining the optimal levels of decomposition, the entropy is evaluated at each level. For a new level
j, the entropy works as the following constraint:
A two-level decomposition method is sufficient for the effective representation of HVDC transmission system identifying the type of fault. The components (low- and high-frequency components) were scaled by their respective gains and then added together to generate the control signal
u:
where gains
k d 1 ,
k d 2 ,…,
k d N are used to tune the high- and medium-frequency components of the fault (instantaneous power) signal (
e d 1 ,
e d 2 ,…,
e d N ). Gain
k a N is used to tune the low-frequency components of the fault signal (
e a N ) under test and
N is the number of decomposition levels.
Numerical simulation results and discussion
For numerical verifications the following parameters are considered and fault occurrences are numerically designed with time intervals as described in
Table 1. The DC transmission line length equals 300 km, and the AC generator was rated at 5000 MVA at 60 Hz, and load end utility of 500 kV. The transformers are rated, the rectifier and inverter ends at 1200 MVA, with grid 345 kV, 50 Hz, 10,000 MVA, and power transmission capacity of 1000 MW.
In the first investigation test,
Fig. 2 shows the simulation response when the 12-pulse LCC-HVDC transmission system is subjected to healthy and single-line-to-ground fault on the generator side by DWT diagnostic tool behavior.
Figure 2a–d depict the three-phase generated voltage, generated currents, DC-link voltage, and DC-link current, respectively. From the results it is clear that healthy condition exists until the time interval 1.6 s, where the designed fault occurs in the transmission system, eventually leading voltages and currents to behave abruptly above the set ratings until 1.7 s, where again it returns back to healthy conditions as designed for investigation.
Figure 2e illustrates the behavior response of fault identification by DWT; it is clearly observed until the healthy conditions output reaches a constant amplitude of 1.7, for all co-efficients of two-level decomposition according to
eq. (6). Once, the designed fault occurs at 1.6 s, the DWT output value increases and reaches the peak amplitude of 6 and the contour area widens as expected.
From the amplitude of peak and contour areas, it could be easily distinguished that the fault that occurred is a single-line-to-ground fault on the generator side. Furthermore, DWT returns back to its initial values once the fault is cleared at 1.7 s
(eq. 6), and the contour area also reduces as it appears in healthy conditions. Hence, by DWT spectrum behavior, the healthy and faulty conditions are clearly distinguishable when the system is subjected to the disturbance.
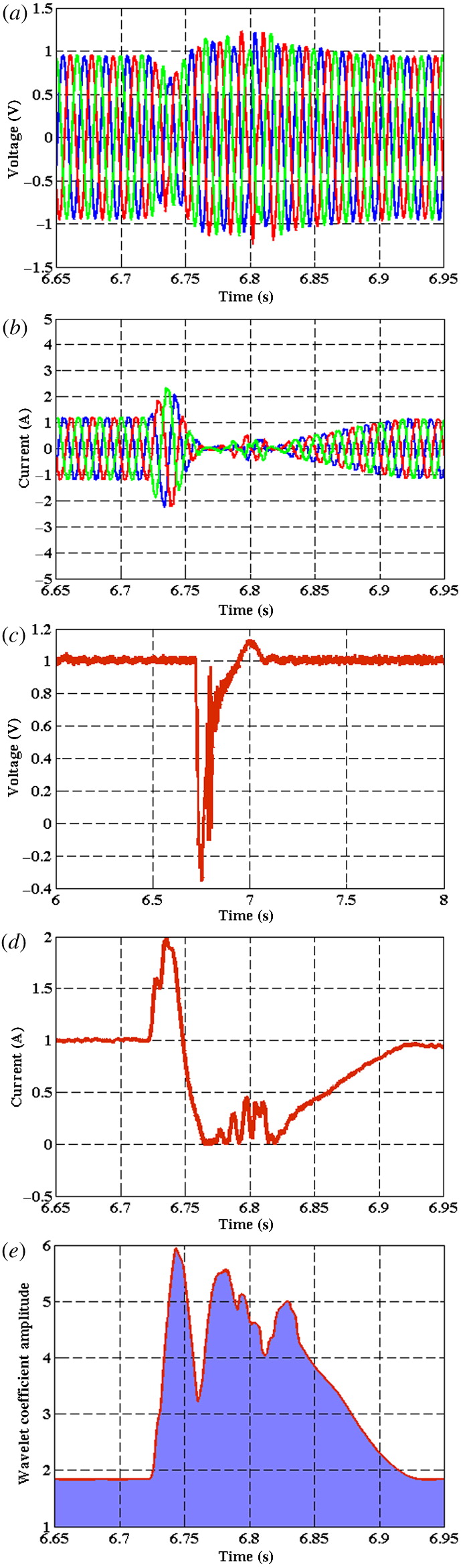
The second investigation test is focused on single-line-to-ground fault identification by DWT on the load end.
Figure 3 describes the simulation response, as a 12-pulse LCC-HVDC transmission system subjected to healthy and single-line-to-ground fault on the load side, and DWT diagnostic tool behavior.
Figure 3a–d depict the three-phase generated voltage, generated currents, DC-link voltage, and DC-link current, respectively. It was clear from the results that healthy conditions exist until the time 6.72 s, where the designed fault occurs in the transmission system, eventually leading the voltages and currents to behave abruptly as predicted above the set ratings until the time of 6.8 s, where again it returns back to healthy conditions as designed for investigation. Behavior of fault identification by DWT is described in
Fig. 3e; it is notable until healthy conditions output reaches a constant amplitude of 1.7, all co-efficient of two-level decomposition according to
eq. (6). Once, the fault occurs at 6.72 s, the DWT output value increases and reaches the peak of 5.8 in amplitude and the contour area widens as expected.
Furthermore, the contour area generated by DWT outputs is not similar to the first investigation test and it is clearly distinguishable. Hence, the amplitude of peak and contour areas shows that the fault occurred is single-line-to-ground fault on load end. DWT returns back to its initial values once the fault is cleared at 6.8 s
(eq. 6) and the contour area also reduces as it appears in healthy conditions. Hence, again by DWT spectrum behavior, the healthy and faulty conditions are clearly predictable when the system subjected to the disturbance.
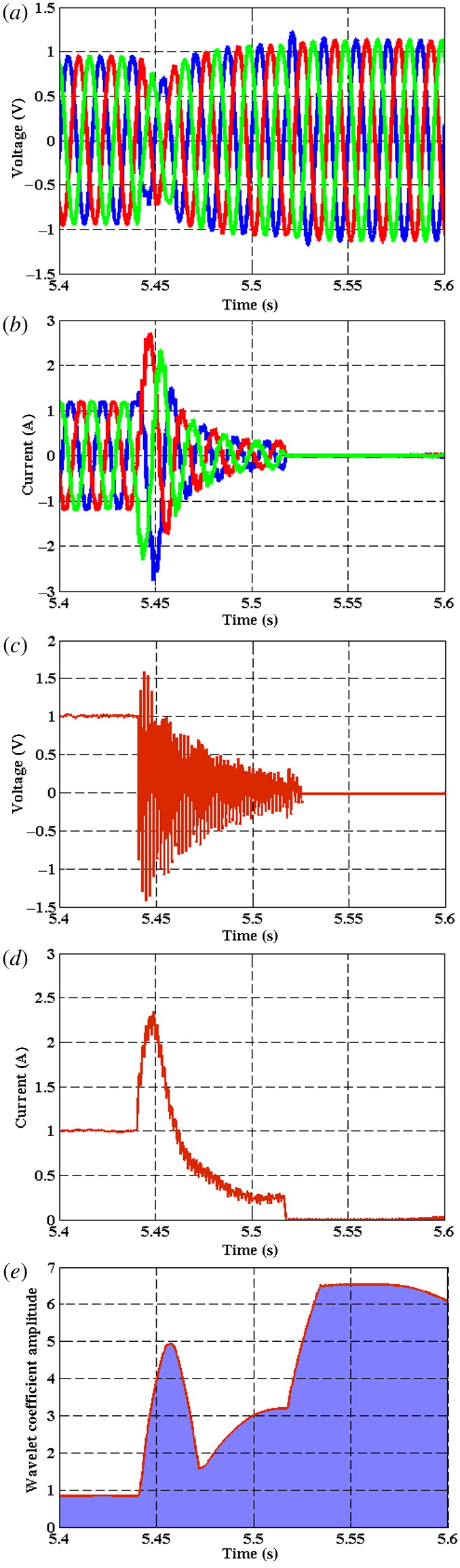
In the third investigation test,
Fig. 4 describes the simulation response, as a 12-pulse LCC-HVDC transmission system subjected to healthy and DC-link fault, and DWT diagnostic tool behavior.
Figure 4a–d depict the three-phase generated voltage, generated currents, DC-link voltage, and DC-link current, respectively. It is noticed from the results that healthy conditions exist until the time interval 5.44 s, where the designed fault occurs in the transmission system, eventually leading the voltages and currents to behave abruptly as predicted above the set ratings until 5.52 s.
Figure 4e elaborates the behavior of fault identification by DWT; it is observed until healthy conditions output reaches a constant amplitude of 1.7, all co-efficient of two-level decomposition according to
eq. (6). Once, the fault occurs at 5.44 s, the DWT output value increases and reaches the peak of 5.8 in amplitude and the contour area widens as expected. To be noted, that the contour area generated by DWT outputs is not similar to the first and second investigation tests and it is clearly distinguishable.
Furthermore, it should be noted that once the DC fault occurs at time interval 5.52 s, drastic failure occurs and the complete system needs to be protected. So, the generator side is open-circuited from DC link similar to the load side; therefore, the AC generator, rectifier, and inverter on the load side are protected. However, voltage generated after the time 5.52 s is purely open-circuited (
Fig. 4a), whereas three-phase current on the generator side, DC-link voltage, and DC-link current are null, which confirms the protection and open-circuited conditions. Hence, the amplitude of peak and contour areas shown by DWT confirm that the fault occurred is DC-link fault on the load end and also the open-circuit protection state. It is concluded from these three preliminary investigation tests that DWT is capable of predicting a diagnostic tool when the HVDC transmission system suffers with different faults.