Cautions on using the Before-After-Control-Impact design in environmental effects monitoring programs
Abstract
Introduction
Methods
Case study
Study sites
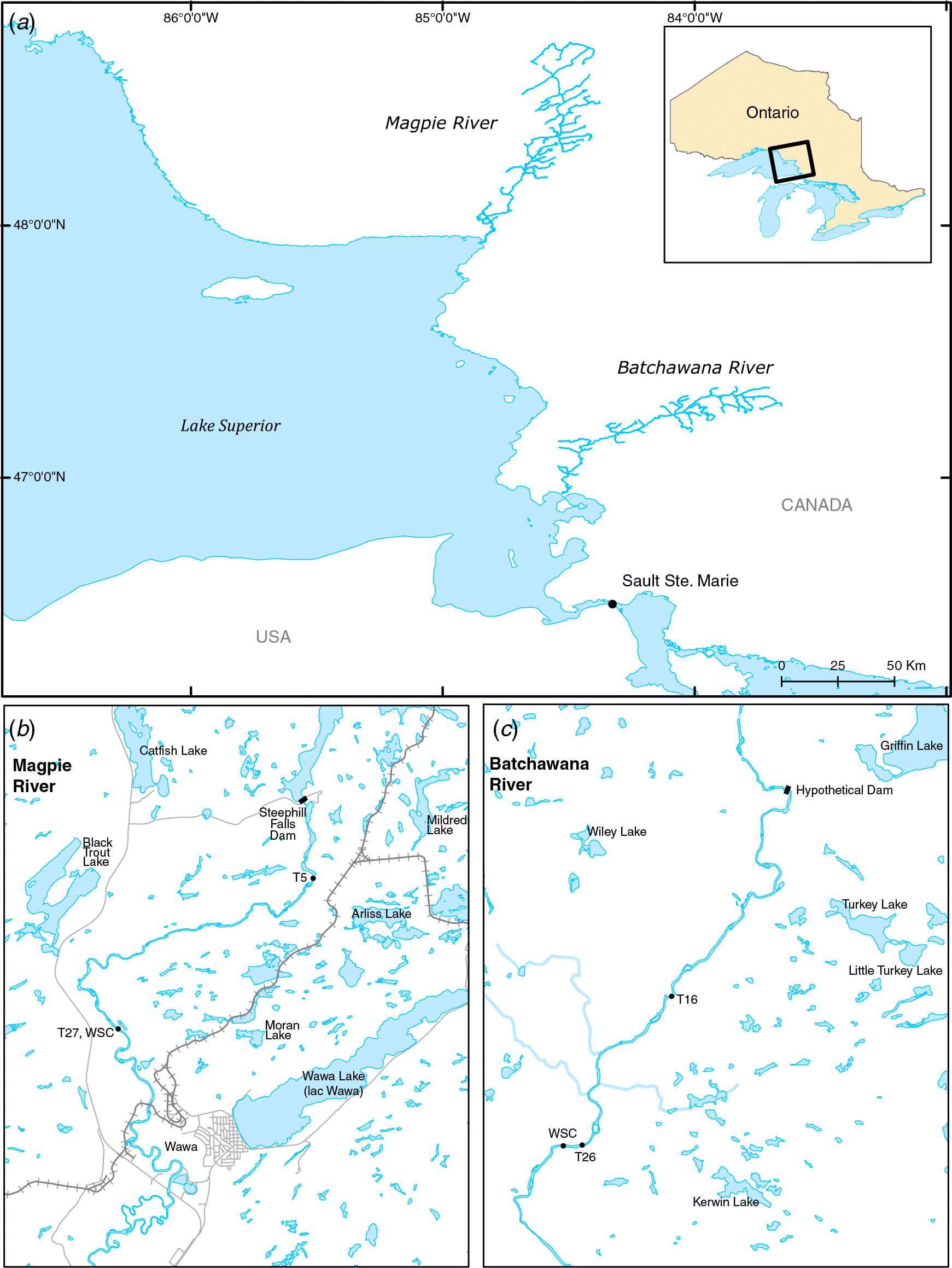
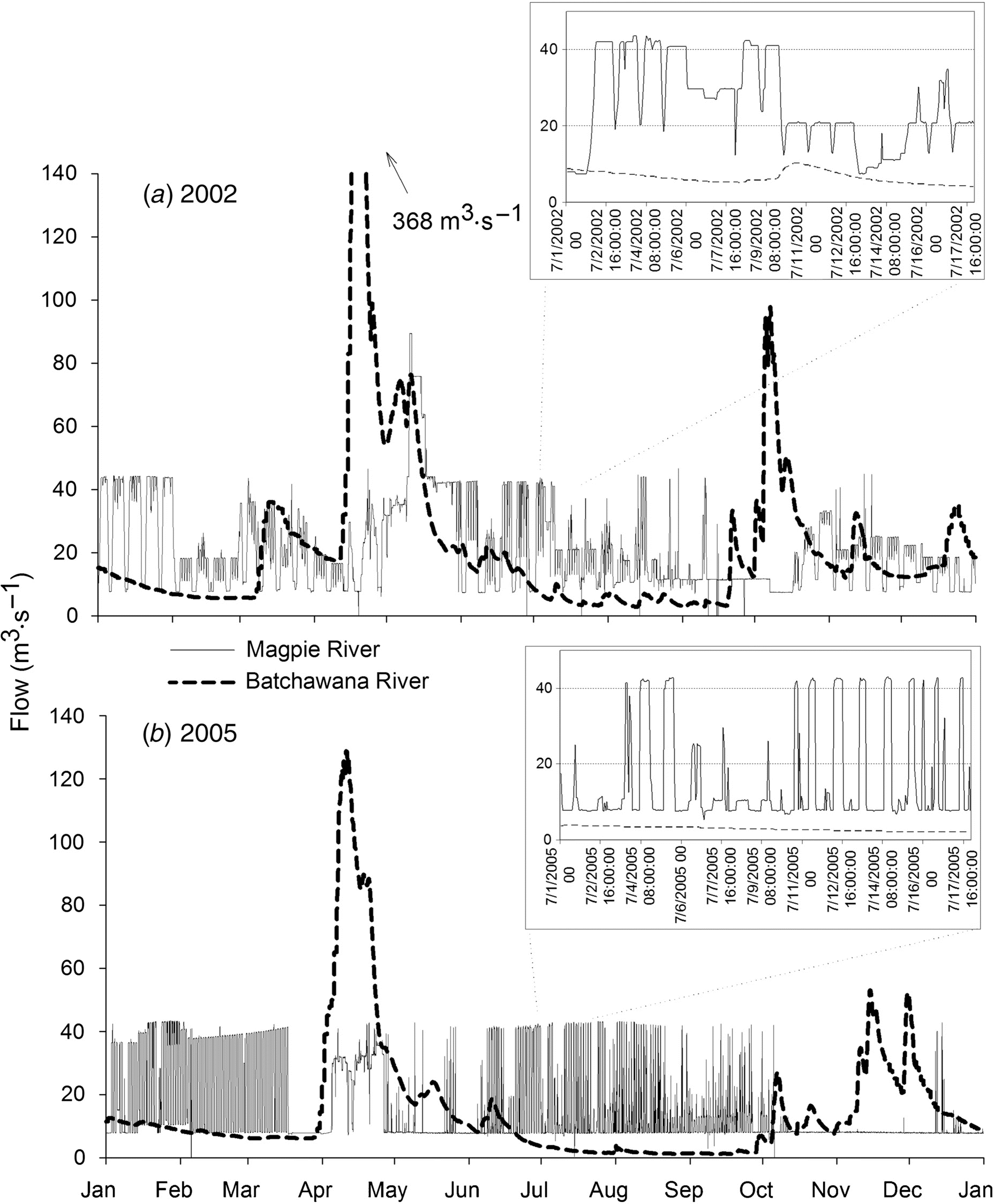
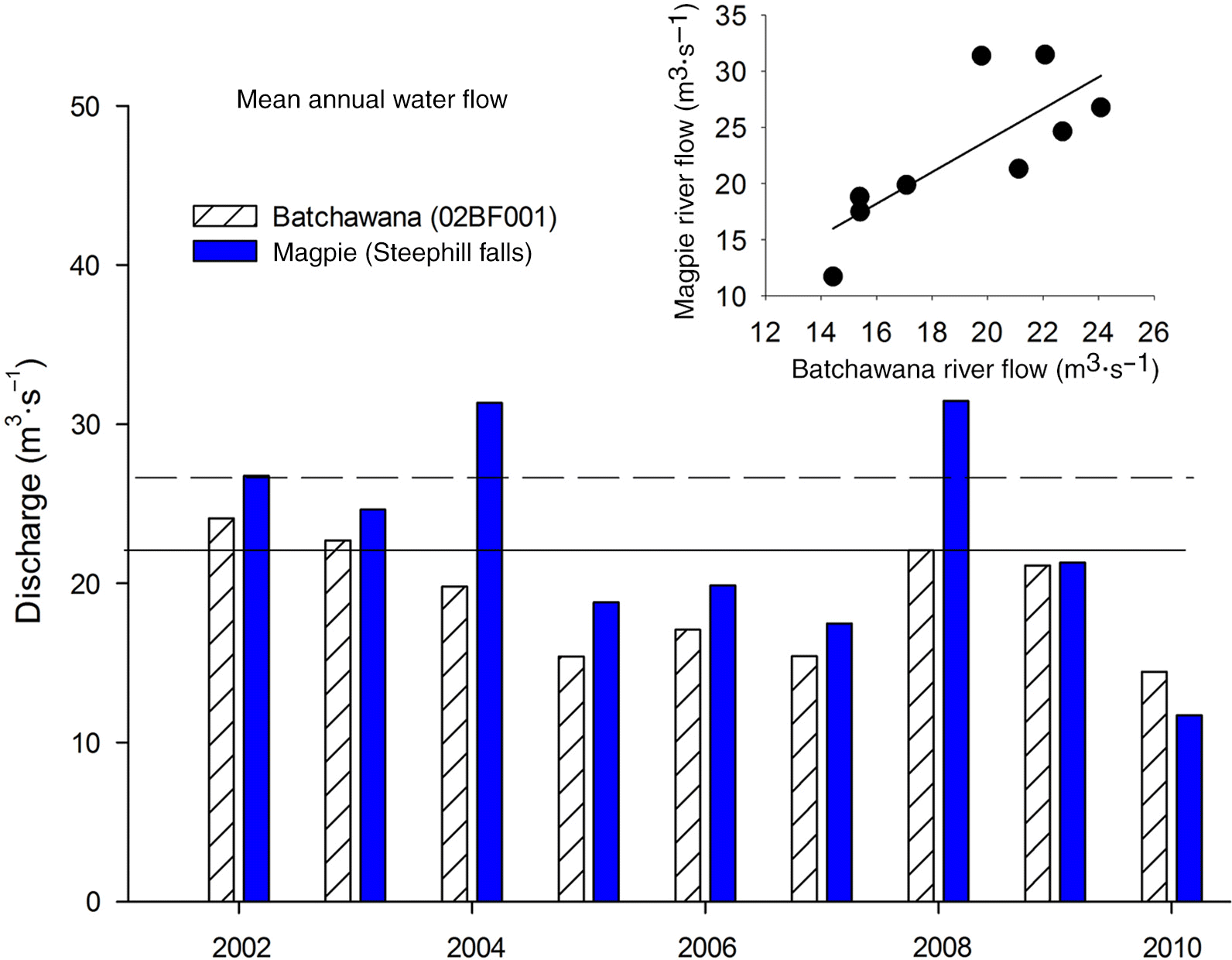
Field sampling
Statistical analysis
Permitting
Results
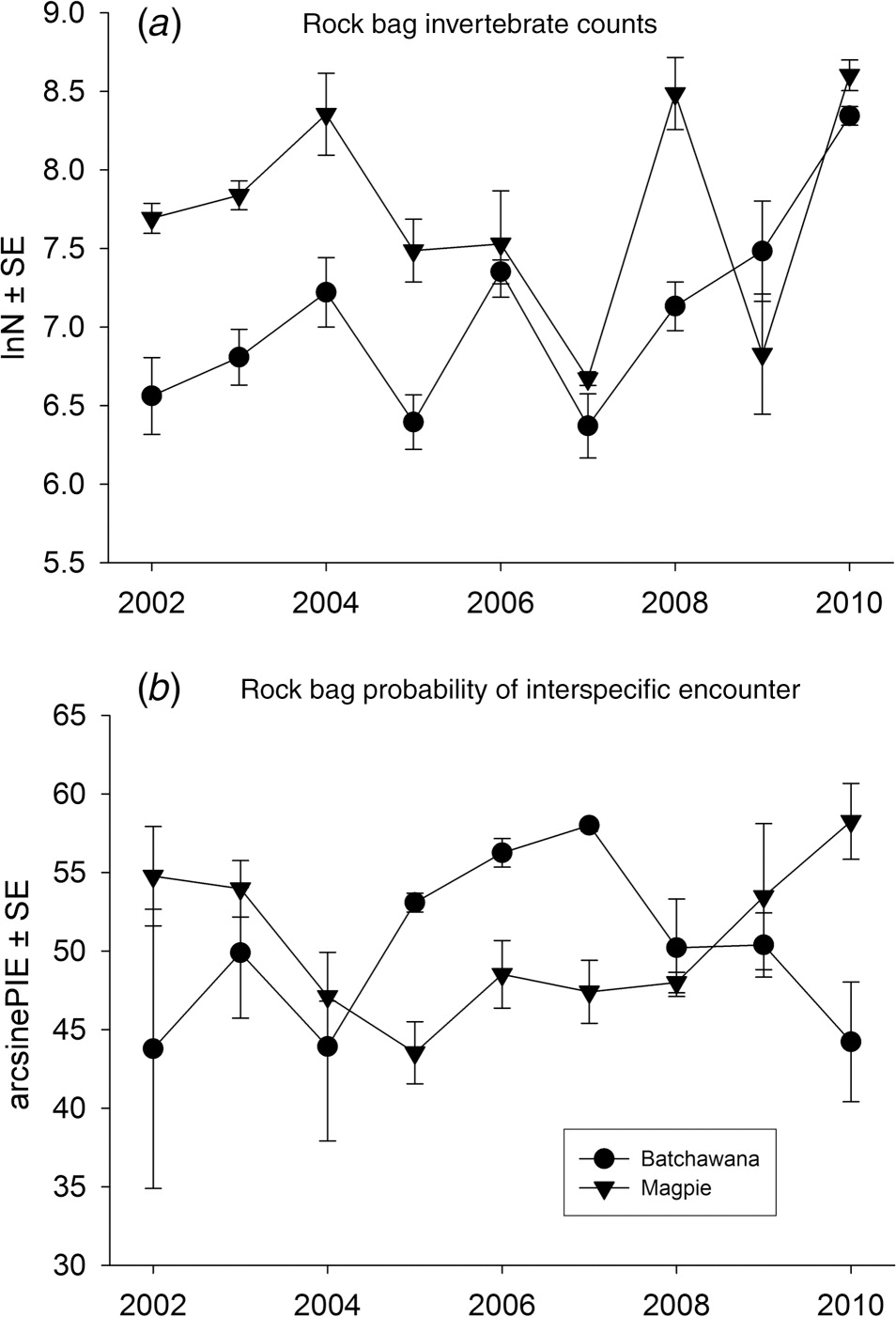
| After years included | SS | F (df) | p | p crit | |
|---|---|---|---|---|---|
| Invertebrate lnN BACI | |||||
| 1, 2, 3, 4, 5, 6 | Long-term unbalanced | 1.8 | 3.8(1,66) | 0.05 | — |
| 1, 2, 3 | Short-term balanced | 1.1 | 4.3(1,48) | 0.04 | — |
| 4, 5, 6 | Long-term balanced | 1.6 | 4.3(1,40) | 0.04 | 0.0125 |
| Invertebrate arcsinePIE BACI | |||||
| 1, 2, 3, 4, 5, 6 | Long-term unbalanced | 412.5 | 6.7(1,66) | 0.01 | 0.01 |
| 1, 2, 3 | Short-term balanced | 824.1 | 13.4(1,48) | <0.001 | 0.008 |
| 4, 5, 6 | Long-term balanced | 6.5 | 0.08(1,40) | 0.78 | — |
Note: In all cases the Before period included 2002–2004. Years included in the After period varied as indicated, where 1 = 2005, 2 = 2006, 3 = 2007, 4 = 2008, 5 = 2009, and 6 = 2010. p crit provides the critical p-value as adjusted by the Holm–Bonferroni method for determining significance, where in this case the total number of tests was 6. Bold text indicates a significant difference.
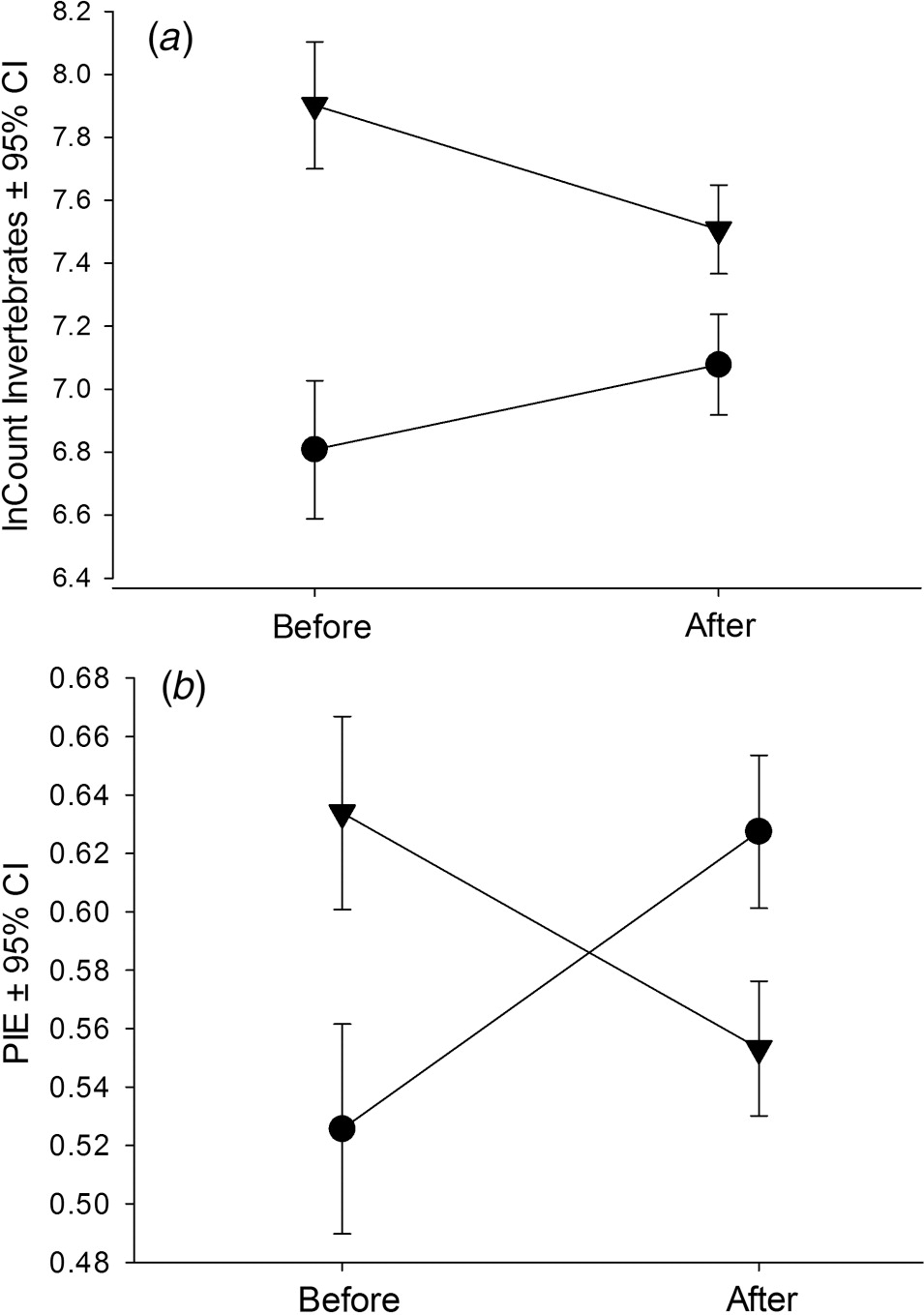
| Source of variation—invertebrates | Mean difference Before ± SE (n) | Mean difference After ± SE (n) | t | p | p crit |
|---|---|---|---|---|---|
| lnN (1, 2, 3, 4, 5, 6) | 1.1 ± 0.13 (13) | 0.43 ± 0.17 (22) | 2.7 | 0.01 | 0.0125 |
| lnN (1, 2, 3) | 1.1 ± 0.13 (13) | 0.51 ± 0.16 (13) | 2.8 | <0.01 | 0.01 |
| lnN (4, 5, 6) | 1.1 ± 0.13 (13) | 0.32 ± 0.35 (9) | 2.4 | 0.03 | 0.025 |
| arcsinePIE (1, 2, 3, 4, 5, 6) | 6.5 ± 3.4 (13) | −3.5 ± 2.1 (22) | 2.6 | 0.01 | 0.017 |
| arcsinePIE (1, 2, 3) | 6.5 ± 3.4 (13) | −9.4 ± 1.2 (13) | 4.4 | <0.001 | 0.008 |
| arcsinePIE (4, 5, 6) | 6.5 ± 3.4 (13) | 5.0 ± 3.2 (9) | 0.32 | 0.75 | — |
Note: In all cases the Before period included 2002–2004. Years included in the After period varied as indicated, where 1 = 2005, 2 = 2006, 3 = 2007, 4 = 2008, 5 = 2009, and 6 = 2010. p crit provides the critical p-value as adjusted by the Holm–Bonferroni method for determining significance. Bold text indicates a significant difference from before to after the change in dam operations.
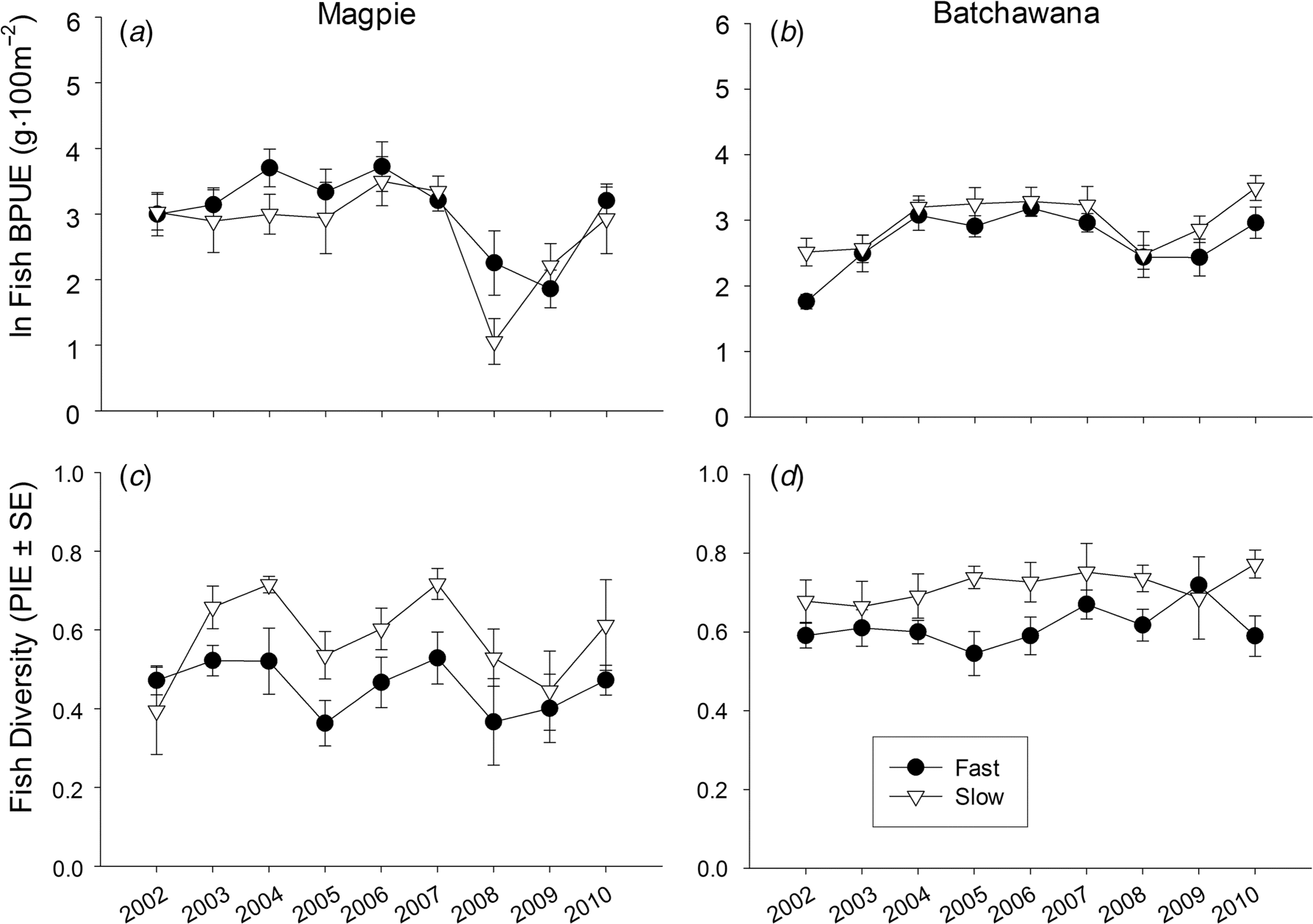
| After years included | Design type | Habitat | SS | F (df) | p | p crit |
|---|---|---|---|---|---|---|
| Fish lnBPUE BACI | ||||||
| 1, 2, 3, 4, 5, 6 | Long-term unbalanced | Fast | 4.2 | 5.5(1,140) | 0.02 | — |
| 1, 2, 3, 4, 5, 6 | Long-term unbalanced | Slow | 3.4 | 3.3(1,132) | 0.07 | — |
| 1, 2, 3 | Short-term balanced | Fast | 1.1 | 2.0(1,92) | 0.16 | — |
| 1, 2, 3 | Short-term balanced | Slow | 0.34 | 0.45(1,88) | 0.50 | — |
| 4, 5, 6 | Long-term balanced | Fast | 6.1 | 7.9(1,92) | 0.006 | — |
| 4, 5, 6 | Long-term balanced | Slow | 7.3 | 7.8(1,84) | 0.006 | 0.004 |
| Fish arcsinePIE BACI | ||||||
| 1, 2, 3, 4, 5, 6 | Long-term unbalanced | Fast | 123 | 0.95(1,140) | 0.33 | — |
| 1, 2, 3, 4, 5, 6 | Long-term unbalanced | Slow | 311 | 1.4(1,132) | 0.23 | — |
| 1, 2, 3 | Short-term balanced | Fast | 14.9 | 0.15(1,90) | 0.69 | — |
| 1, 2, 3 | Short-term balanced | Slow | 95 | 0.57(1,88) | 0.45 | — |
| 4, 5, 6 | Long-term balanced | Fast | 237 | 1.7(1,92) | 0.19 | — |
| 4, 5, 6 | Long-term balanced | Slow | 453.8 | 1.7(1,84) | 0.19 | — |
Note: In all cases the Before period included 2002–2004. Years included in the After period varied as indicated, where 1 = 2005, 2 = 2006, 3 = 2007, 4 = 2008, 5 = 2009, and 6 = 2010. p crit provides the critical p-value as adjusted by the Holm–Bonferroni method for determining significance, where in this case the total number of tests was 12.
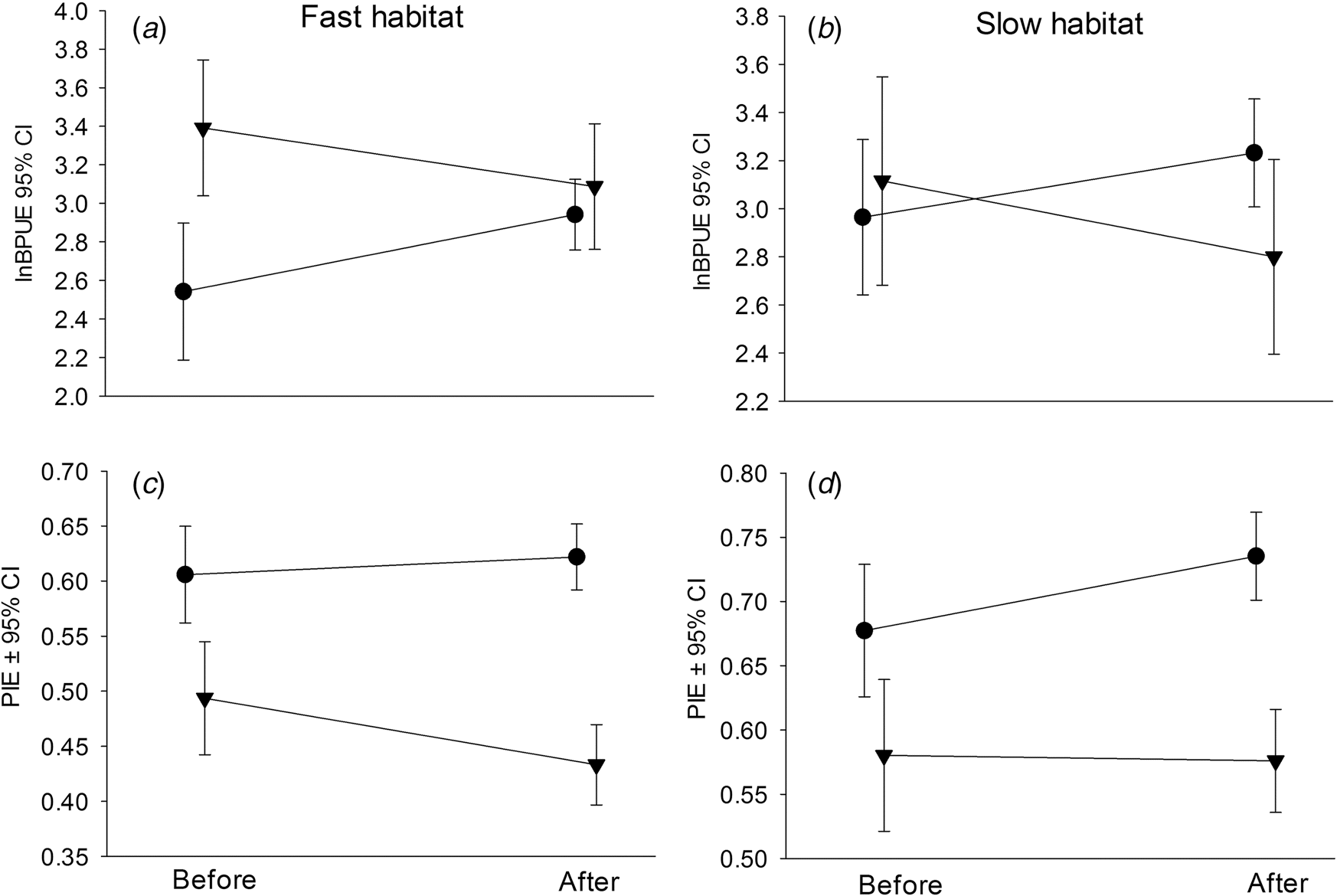
| Source of variation—fish lnBPUE or diversity (arcsinePIE) | Habitat | Mean difference Before ±SE (n) | Mean difference After ±SE (n) | t | p | p crit |
|---|---|---|---|---|---|---|
| lnBPUE (1, 2, 3, 4, 5, 6) | Fast | 0.84 ± 0.20 (24) | 0.12 ± 0.16 (46) | 2.6 | 0.01 | 0.005 |
| Slow | 0.25 ± 0.22 (22) | −0.43 ± 0.20 (46) | 2.0 | 0.05 | — | |
| lnBPUE (1, 2, 3) | Fast | 0.84 ± 0.20 (24) | 0.40 ± 0.19 (24) | 1.6 | 0.12 | — |
| Slow | 0.25 ± 0.22 (22) | 0.005 ± 0.23 (24) | 0.69 | 0.49 | — | |
| lnBPUE (4, 5, 6) | Fast | 0.84 ± 0.20 (24) | −0.17 ± 0.26 (24) | 3.1 | 0.003 | 0.0045 |
| Slow | 0.25 ± 0.23 (22) | −0.90 ± 0.28 (22) | 3.2 | 0.003 | 0.004 | |
| arcsinePIE (1, 2, 3, 4, 5, 6) | Fast | −8.5 ± 2.6 (24) | −12.5 ± 2.6 (48) | 0.96 | 0.34 | — |
| Slow | −5.6 ± 4.0 (22) | −12.1 ± 3.1 (46) | 1.2 | 0.22 | — | |
| arcsinePIE (1, 2, 3) | Fast | −8.5 ± 2.6 (24) | −10.1 ± 3.1 (24) | 0.39 | 0.70 | — |
| Slow | −5.6 ± 4.0 (22) | −9.7 ± 2.5 (24) | 0.88 | 0.38 | — | |
| arcsinePIE (4, 5, 6) | Fast | −8.5 ± 2.6 (24) | −14.8 ± 4.1 (24) | 1.3 | 0.20 | — |
| Slow | −5.6 ± 4.0 (22) | −14.7 ± 5.8 (22) | 1.3 | 0.20 | — |
Note: In all cases the Before period included 2002–2004. Years included in the After period varied as indicated, where 1 = 2005, 2 = 2006, 3 = 2007, 4 = 2008, 5 = 2009, and 6 = 2010. p crit provides the critical p-value as adjusted by the Holm–Bonferroni method for determining significance. Bold text indicates a significant difference from before to after the change in dam operations.
| After years included | SS | F (df) | p | p crit | |
|---|---|---|---|---|---|
| Invertebrate lnN BACI | |||||
| 1, 3, 6 | BA × CI | 0.91 | 1.9(1,46) | 0.17 | — |
| 2, 4, 6 | BA × CI | 0.82 | 3.0(1,42) | 0.09 | — |
| 1, 3, 5 | BA × CI | 1.8 | 7.0(1,46) | 0.01 | 0.01 |
| Invertebrate arcsinePIE BACI | |||||
| 1, 3, 6 | BA × CI | 351.9 | 4.4(1,46) | 0.04 | 0.0125 |
| 2, 4, 6 | BA × CI | 104.3 | 1.3(1,42) | 0.26 | — |
| 1, 3, 5 | BA × CI | 556.8 | 7.9(1,46) | 0.007 | 0.008 |
Note: In all cases the Before period included 2002–2004. Years included in the After period varied as indicated, where 1 = 2005, 2 = 2006, 3 = 2007, 4 = 2008, 5 = 2009, and 6 = 2010. p crit provides the critical p-value as adjusted by the Holm–Bonferroni method for determining significance. Bold text indicates a significant difference.
| After years included | Habitat | SS | F (df) | p | p crit |
|---|---|---|---|---|---|
| Fish lnBPUE BACI | |||||
| 1, 3, 6 | Fast | 1.7 | 3.2(1,92) | 0.08 | — |
| 1, 3, 6 | Slow | 1.3 | 1.7(1,86) | 0.20 | — |
| 2, 4, 6 | Fast | 2.4 | 3.1(1,92) | 0.08 | — |
| 2, 4, 6 | Slow | 4.0 | 3.6(1,86) | 0.06 | — |
| 1, 3, 5 | Fast | 3.9 | 5.6(1,92) | 0.02 | 0.004 |
| 1, 3, 5 | Slow | 1.5 | 1.9(1,86) | 0.17 | — |
| Fish arcsinePIE BACI | |||||
| 1, 3, 6 | Fast | 25.6 | 0.28(1,92) | 0.60 | — |
| 1, 3, 6 | Slow | 78.7 | 0.38(1,86) | 0.54 | — |
| 2, 4, 6 | Fast | 21.6 | 0.16(1,92) | 0.69 | — |
| 2, 4, 6 | Slow | 190.2 | 0.94(1,86) | 0.34 | — |
| 1, 3, 5 | Fast | 213.5 | 2.1(1,92) | 0.15 | — |
| 1, 3, 5 | Slow | 285.3 | 1.2(1,86) | 0.27 | — |
Note: In all cases the Before period included 2002–2004. Years included in the After period varied as indicated, where 1 = 2005, 2 = 2006, 3 = 2007, 4 = 2008, 5 = 2009, 6 = 2010. p crit provides the critical p-value as adjusted by the Holm–Bonferroni method for determining significance.
| Test | Habitat | lnN/Fish BPUE F (df), p, (trend) | arcsinePIE F (df), p, (trend) | p crit |
|---|---|---|---|---|
| Invertebrates Before-After (no Control) | 2.6(1,33), 0.12, (↓) | 2.6(1,33), 0.11, (↓) | — | |
| Invertebrates Control-Impact (no Before) | 3.2(1,42), 0.08, (↑) | 4.0(1,42), 0.05, (↓) | 0.0125 | |
| Fish Before-After (no Control) | Fast | 1.9(1,70), 0.18, (↓) | 0.32(1,70), 0.57, (↓) | — |
| Slow | 0.87(1,66), 0.35, (↓) | 0.004(1,66), 0.95, (↔) | — | |
| Fish Control-Impact (no Before) | Fast | 0.41(1,94), 0.52, (↑) | 24.0(1,94), <0.001, (↓) | 0.00625 |
| Slow | 3.5(1,90), 0.06, (↓) | 15.6(1,90), <0.001, (↓) | 0.007 |
Note: The trend arrow indicates the directional difference (increasing or decreasing) between the mean values from Before to After or between Control and Impact. p crit provides the critical p-value as adjusted by the Holm–Bonferroni method for determining significance, where in this case the total number of tests was 4 for invertebrates and 8 for fish.
Discussion
Acknowledgements
References
Information & Authors
Information
Published In

History
Copyright
Data Availability Statement
Key Words
Sections
Subjects
Authors
Author Contributions
Competing Interests
Metrics & Citations
Metrics
Other Metrics
Citations
Cite As
Export Citations
If you have the appropriate software installed, you can download article citation data to the citation manager of your choice. Simply select your manager software from the list below and click Download.
