Strategies to prevent damage to critical infrastructure due to induced seismicity
Abstract
There has been a significant increase in the rate of felt earthquakes in western Alberta and eastern British Columbia, which has been associated with hydraulic fracturing and wastewater disposal. The increased rate of seismicity and the potential for localized strong ground motions from very shallow events poses an increased hazard to critical infrastructure such as major dams—particularly for older high-consequence structures. This paper overviews the factors that affect the likelihood of damaging ground motions and examines their implications for hazard assessment and mitigation. A strategy aimed at reducing the likelihood of potentially damaging ground motions to achieve probabilistic targets for critical facilities is developed, comprising elements of both mitigation and avoidance. For critical facilities, an effective strategy includes (i) an exclusion zone having a radius of ∼5 km; and (ii) a monitoring-and-response protocol to track the rate of events at the M > 2 level within 25 km, with adjustment of operational practices if required. An exclusion zone provides a deterministic safety margin to ensure the integrity of those few facilities for which failure consequences are unacceptable. Real-time monitoring tied to a response protocol can be used to control the rate of significant events and thereby limit the hazard more broadly.
Introduction
Induced seismicity is the occurrence of earthquakes that are triggered by industrial processes including energy technologies, mining, and reservoir impoundment. Induced seismicity has recently become a pressing global problem. Improvements in hydraulic fracturing and horizontal drilling have unlocked tight reservoirs around the world, ushering in a new oil and gas boom. The rise in the unconventional production of oil and gas has been coupled with a dramatic increase in the rate of seismicity in many parts of central North America in the last 5–10 years (Ellsworth 2013; Atkinson et al. 2016). Most oil and gas operations do not trigger seismicity above the felt threshold, but a small percentage of operations trigger events large enough to be felt (National Research Council 2013), and an even smaller percentage trigger potentially damaging events. For example, events as large as M 5.6–5.8 (where M is moment magnitude) are thought to have been triggered by deep disposal of fluids, in the 2011 Prague and 2016 Pawnee sequences in Oklahoma (e.g., Keranen et al. 2013). The basic mechanism of induced seismicity is widely agreed upon: it is caused by a change in pore fluid pressure and (or) a change in the state of stress, which may cause re-activation of existing faults or fractures. However, we cannot currently predict the likelihood or magnitude of such events from specific planned operations (in a deterministic sense) because we do not have enough data on the complex natural rock systems, nor do we have validated predictive models.
This paper develops an approach to assess and mitigate the hazard from induced seismicity to infrastructure, with an emphasis on high-consequence infrastructure such as major dams. The approach is developed by performing a statistically based assessment of the hazard, including its uncertainty. Mitigation and avoidance strategies are developed that can be used to reduce the hazard to meet specified targets. Due to the high consequences of failure for some structures such as major dams, applicable safety guidelines mandate that they should be capable of withstanding earthquake ground motions having a probability of no greater than 0.0001 per annum (1/10 000 p.a.) (e.g., Canadian Dam Association 2007). The initiation of oil and gas activity close to critical facilities, with an uncertain likelihood of induced seismicity, may make it very difficult to achieve the required safety objectives. Moderate events very nearby could cause potentially damaging motions. The likelihood of damaging motions depends on the likelihood of event initiation, the characteristics of event sequences, the ground motion characteristics, and the response characteristics of the structure. The uncertainties in quantifying these factors are large, causing a major challenge in meeting the 1/10 000 p.a. seismic reliability objectives with satisfactory confidence.
In this paper, the key factors that influence hazard are explored within the framework of seismic hazard assessment, and mitigation or avoidance strategies are developed accordingly. Such strategies can be placed within the overall context of the risk matrix approach of Walters et al. (2015), in which operations may be considered to be in a red, yellow, or green zone (following a traffic light analogy) depending on operational factors and exposure. Over time, as our knowledge of the processes that control the hazard improve, and uncertainties in hazard assessment are reduced, it may be feasible to significantly revise or refine these strategies. The current document is intended as interim guidance to ensure the integrity of critical infrastructure.
Elements of the seismic hazard framework for induced seismicity
Seismic hazard is generally assessed probabilistically, following the probabilistic seismic hazard analysis (PSHA) framework developed by Cornell (1968) and McGuire (2004); this is the framework used for building codes in Canada and the US (e.g., Petersen et al. 2008, 2015; Halchuk et al. 2014), as well as for standards for critical facilities such as dams and nuclear power plants (e.g., Canadian Dam Association Guidelines 2013). The PSHA assesses the likelihood of exceeding specified levels of ground motion. For new buildings and structures, the PSHA can be used to determine the level of seismic resistance required for design. For existing structures, the PSHA can be used to determine whether target seismic reliability objectives are being met, if the capacity of the structure is known. The required input parameters for the analysis are (i) characterization of earthquake source zones that contribute significant hazard to the site; (ii) the rate of earthquakes of different magnitude levels for all earthquake source zones; (iii) the minimum and maximum magnitude of earthquakes to be considered for each source; and (iv) the ground motions that will result as a function of magnitude and distance, for a reference site condition. The uncertainties in these inputs also need to be defined. The output is a set of hazard curves that show ground motion amplitudes, for selected ground motion parameters, as a function of probability of exceedance, along with their confidence limits.
In this section, a hazard model for induced seismicity in western Canada is presented considering each of these elements. Only the induced seismicity hazard is considered here. The natural hazard is neglected for simplicity, although in reality, it is the sum of the natural and induced hazards that must be accommodated. By neglecting the natural hazard, we are implicitly assuming the induced seismicity hazard is the dominant contribution to hazard. We therefore consider a single source zone—an areal source that encompasses oil and gas operations, which are assumed to surround a site of interest. For forecasting potential hazard due to future operations, it is important to quantify the likelihood that such operations will trigger seismicity, so that this activation probability can be included in the analysis—it is a key source characteristic for postulated induced seismicity sources.
Source zone characteristics for induced seismicity
The hazard framework is focused on a potential induced seismicity source due to hydraulic fracturing operations in horizontal wellbores and to a lesser extent wastewater disposal. Since about 2008, tight oil and gas reservoirs in western Canada have increasingly been developed by drilling wells horizontally through the reservoir rock, at depths of a few km. The horizontal segment of the well typically extends ∼1.8–3 km, over which distances there is a controlled, high-pressure injection of fluid and proppant to fracture the target formation. Hydraulic fracturing in western Canada has, in some instances, been associated with significant induced seismicity. In the last few years, several sequences of seismicity including events at the M > 4 level have been induced by hydraulic fracturing in western Alberta and northeastern British Columbia (Atkinson et al. 2016; Bao and Eaton 2016; Schultz et al. 2017).
Figure 1 shows the association between oil and gas activity and seismicity in the Western Canada Sedimentary Basin (WCSB) on a regional basis, as determined by Ghofrani and Atkinson (2016) in a statistical study. They subdivided the region into cells of 10 km radius and evaluated for each cell whether there was a relationship between seismicity and hydraulic fracturing in horizontal wells (referred to as HF wells). The rationale for dividing the region into cells was to be able to evaluate susceptibility to seismicity in spatially discrete areas, rather than looking at individual wells. Such an approach is more useful for hazard forecasting in specific areas. Every cell that contains at least one HF well is classed as active, whereas the remainder of the cells are classed as null. A possible temporal correlation between M ≥ 3 seismicity and HF wells is identified if an event (M ≥ 3) occurred in a cell within a window beginning with the commencement of hydraulic fracturing and ending 3 months after the completion of treatment. If an active cell contains at least one event that meets the temporal criterion for correlation, then its grid point is a hit for potential induced seismicity. The total number of hit points (N Hit) and the total number of active cells (N Active) can be used to calculate the ratio Rh 10 = N Hit/N Active, which is an estimate of the regionally averaged probability that operations in a 10 km radius cell may be associated with seismicity. We consider that the quantity R hA is a rough estimate of the prior probability of inducing seismicity by commencing HF operations in a small area in the WCSB in a Bayesian sense; note that the area in this case is that associated with a circle of the given radius (i.e., an area of π(10 km)2 = 314 km2). Based on this logic, and using a Monte Carlo approach to assess the statistical significance of the observed hit rates, Ghofrani and Atkinson (2016) concluded that the regionally averaged likelihood that HF well operations in a 10 km cell will trigger M ≥ 3 seismicity is ∼0.01–0.03. We can normalize this to obtain a per annum rate of M ≥ 3 events in a 10 km radius cell by considering the following conditions: (i) the average number of M ≥ 3 per hit cell = 2.13; (ii) a total of 71 hit cells; and (iii) the hit cells represent a total of 136.5 well years of operation, for the temporal association window of 3 months following each operation. Thus, the cellular activity rate can be normalized to a per annum rate by multiplying it by the factor (2.13)(71)/(136.5) = 1.1, which is near unity. We conclude that the per annum rate of induced M ≥ 3 events is ∼0.01–0.03 for a 10 km cell (i.e., area of 314 km2) in which HF well operations are being performed in the year. This net rate for induced events for HF wells (which includes the activation probability) is a key source parameter in hazard assessments. By expressing it per annum on a per area basis, it is straightforward to define an areal source zone for hazard analysis and specify its recurrence parameters.
Fig. 1.

Recurrence parameters
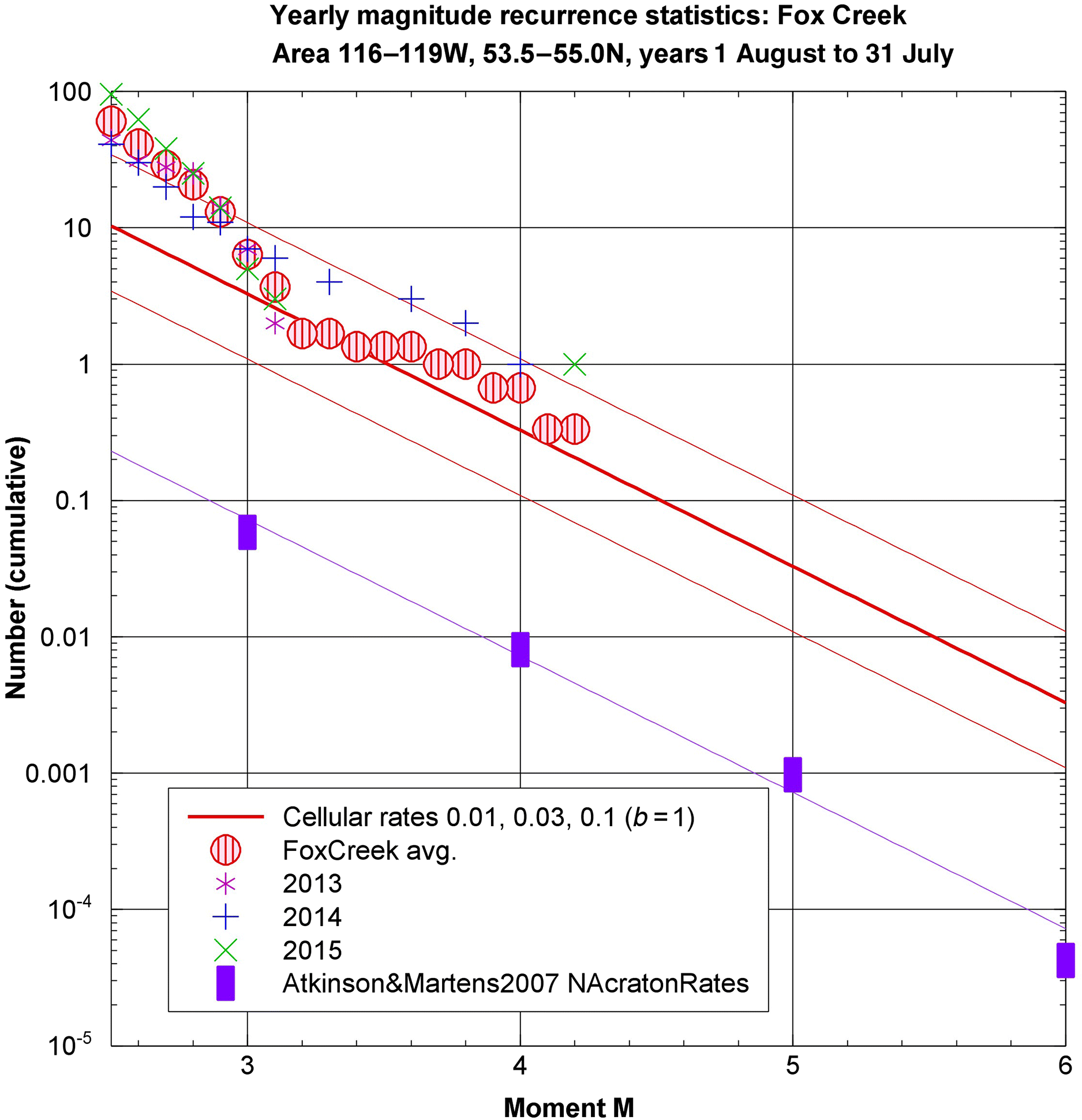
The rate of occurrence of earthquakes of different sizes is expressed by the Gutenberg–Richter relation (Richter 1958), truncated at a maximum magnitude (Mx). Mx is the largest event that is physically possible in the zone. The Gutenberg–Richter relation states that the cumulative number of events of magnitude ≥M, considering events below Mx, is given by log N(≥M) = a − bM, where a is the rate parameter and b is the slope. An example is shown in Fig. 2 for the Fox Creek area of western Alberta (the middle purple box in Fig. 1), in which the average yearly recurrence statistics are shown for 3 years starting in mid-2013, along with the average rates per annum over the 3-year period. The earthquake data for this plot are derived from the Alberta Composite Seismicity Catalog (inducedseismicity.ca). A Gutenberg–Richter relation with the slope b = 1 is plotted for three different rates of activity. The lower two levels of activity correspond to the average cellular per annum rates (cell of 10 km radius) of 0.01 and 0.03 for M ≥ 3, which have been normalized to account for the area of the rectangular source defined for the Fox Creek region (e.g., by multiplying by a factor of (195 km × 165 km)/(π 102)). Note that the defined box containing the Fox Creek region is more active than average for induced seismicity sources in western Canada. The Fox Creek activity rates in the last 3 years are greater than average rates for natural seismicity sources in the North American craton and Canadian shield, as determined by Atkinson and Martens (2007), by nearly a factor of 100. For the induced seismicity hazard analysis, we define a large rectangular box (such as the purple box in Fig. 1) that acts as an induced seismicity source zone and assign it the rate parameters shown in Fig. 2, assuming the middle rate (the cellular rate of 0.03 p.a. for a cell with a 10 km radius).
Fig. 2.
Maximum magnitude
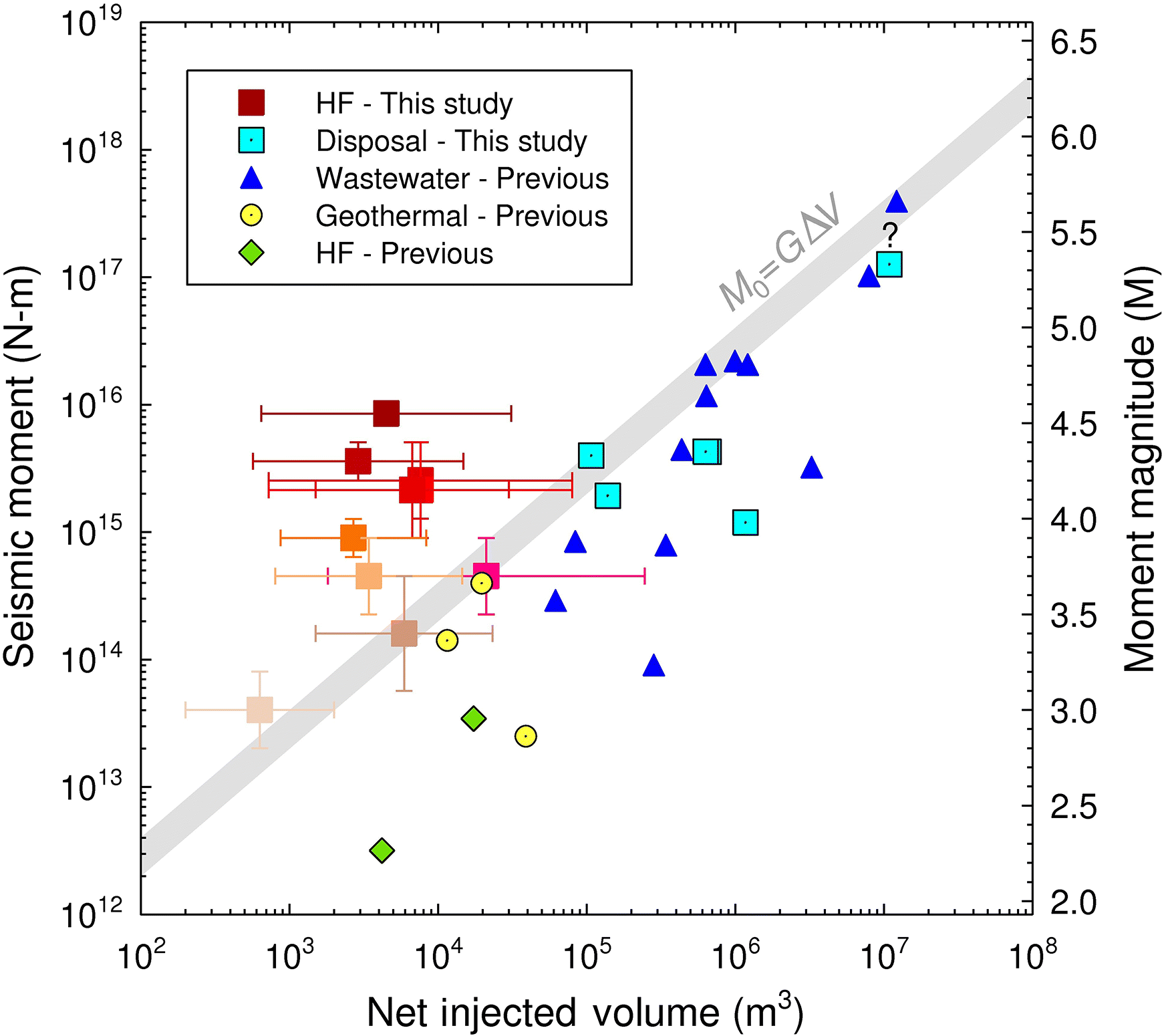
Among the event clusters in the WCSB, there have been several events of M > 4. The largest event attributed to hydraulic fracturing to date was M = 4.6 (Atkinson et al. 2016). The maximum magnitude of the events that could be triggered is not yet known. It has been postulated that for events triggered by fluid disposal, the maximum magnitude may be limited by the cumulative volume of fluid injected into the area (McGarr 2014). However, the hypothesis that magnitude is limited by the injected volume does not appear to hold for earthquakes triggered by hydraulic fracturing in western Canada. This is illustrated in Fig. 3, which shows that several of the larger events triggered by hydraulic fracturing in the WCSB have clearly exceeded the upper bounds established based on injected volume, even if we consider the maximum reasonable uncertainty in both the moment magnitude and the volume of fluid involved.
Fig. 3.
As a general principle, the maximum magnitude is limited by the size of the fault that is re-activated, whereas the expected frequency of large events (relative to small events) can be calculated based on Gutenberg–Richter scaling (Petersen et al. 2015; van der Elst et al. 2016). This is illustrated for seismicity in the WCSB in Fig. 4. The figure shows the number of events of M ≥ 3.5 in 5-year windows, ending at the end of 2016, as listed in the Alberta Composite Catalog (inducedseismicity.ca); the area covered is that from 48° to 53° N and 110° to 121° W, plus the area from 53° to 60° N and 110° to 124° W. In most 5-year windows since 1970, the total number (N) of M ≥ 3.5 events is ∼10, and thus for Gutenberg–Richter scaling (Richter 1958) with a slope (b-value) of 1, we would expect the maximum observed event to be near M = 4.5; in 1 out of 10 such 5-year windows, we would expect the maximum observed to be ∼1 unit higher, or M ∼5.5. Overall this is what we observe. Specifically, the maximum observed magnitude in a time window tends to be larger in windows with more events. The most active window is the most recent (ending at the end of 2016), for which the observed maximum magnitude of 4.6 is just slightly lower than would be expected based on the rate of events.
Fig. 4.
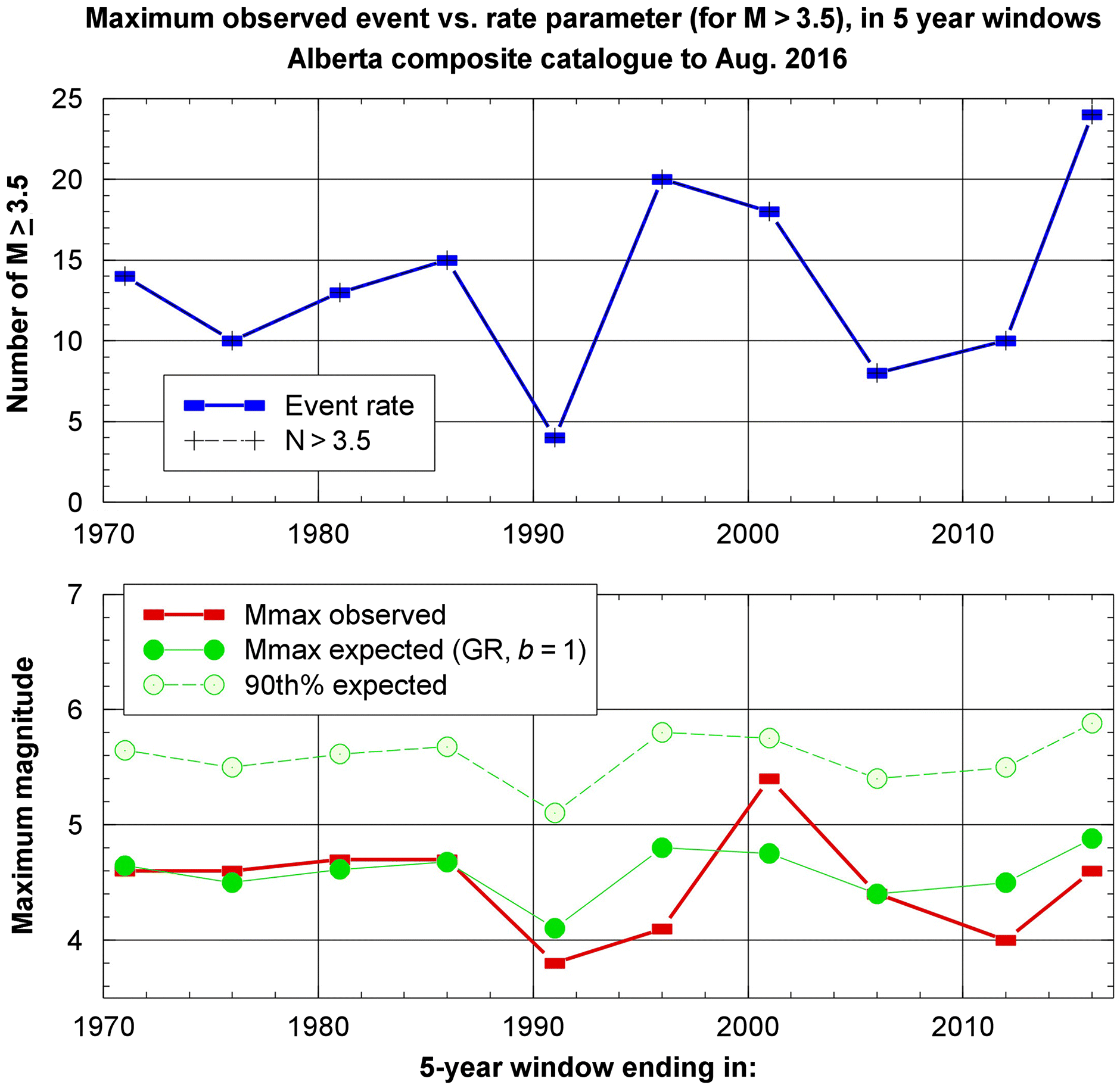
It is important to recognize that the maximum observed values in a time window are not the maximum possible values (Mx). We cannot determine Mx directly from observations because we cannot adequately sample events with low recurrence rates. Maximum possible events may have annual likelihoods of only ∼1/1000, for example, and thus be much greater than the 90th percentile expected values for any given time window (i.e., greater than the 90th percentile values plotted in Fig. 4). Considering that the maximum possible magnitude for induced events is poorly constrained and may not be significantly lower than that for natural events in the region, the hazard analysis will consider a range of possible values for maximum magnitude (Mx), ranging from 5.0 to 6.5. This range is slightly lower than that considered for natural earthquakes in the region (Halchuk et al. 2014). The analysis is not particularly sensitive to reasonable variations in the assumed values of maximum magnitude (Atkinson et al. 2015a).
Ground motions
A key issue in the assessment of hazard from induced seismicity is the specification of ground motion amplitudes associated with induced events, particularly at close distances (within tens of km of the source). These are commonly estimated using ground motion prediction equations (GMPEs) that express peak ground amplitudes and response spectra (5% damped pseudo-spectral acceleration (PSA)) as a function of moment magnitude, distance, and other variables. There is a paucity of well-calibrated and robust GMPEs derived strictly from induced events, although this situation is rapidly changing as new data sets become available. Therefore, induced seismicity hazard applications have tended, of necessity, to draw on models of ground motion amplitudes developed from natural events. This was the rationale for the Atkinson (2015) (denoted A15) GMPE, which examined the magnitude and distance scaling for small-to-moderate events (M 3–6) at hypocentral distances (R hypo) < 40 km. The A15 GMPE was derived by empirical analysis of natural events in California. However, it explicitly addressed the point-source scaling attributes and near-distance saturation behavior expected for induced events, thus providing a middle ground between GMPEs developed entirely for natural events, and GMPEs developed entirely for induced events. A follow-up study (Atkinson and Assatourians 2017) demonstrated that at least three published GMPEs have attributes that make them good proxies for induced earthquakes, as follows: the Atkinson (2015; A15), Yenier and Atkinson (2015; YA15), and Abrahamson et al. (2014; ASK14) GMPEs. (Note that an unspecified depth to top of rupture should be prescribed with ASK14 if it is to be used for this purpose; see Atkinson and Assatourians 2017 for details.)
Figure 5 shows that these GMPEs are appropriate in functional form and overall amplitude level, as they match ground motion observations from induced events in Oklahoma and Alberta. We may, therefore, use these GMPEs to define a representative suite that models amplitudes and their scaling for use in hazard analysis. A two-GMPE suite is used to characterize ground motion amplitudes, as shown in Fig. 5; the upper GMPE is the A15 model, whereas an alternative model has been defined by applying a distance-dependent scaling factor that reduces the motions, especially at very short distances.
Fig. 5.
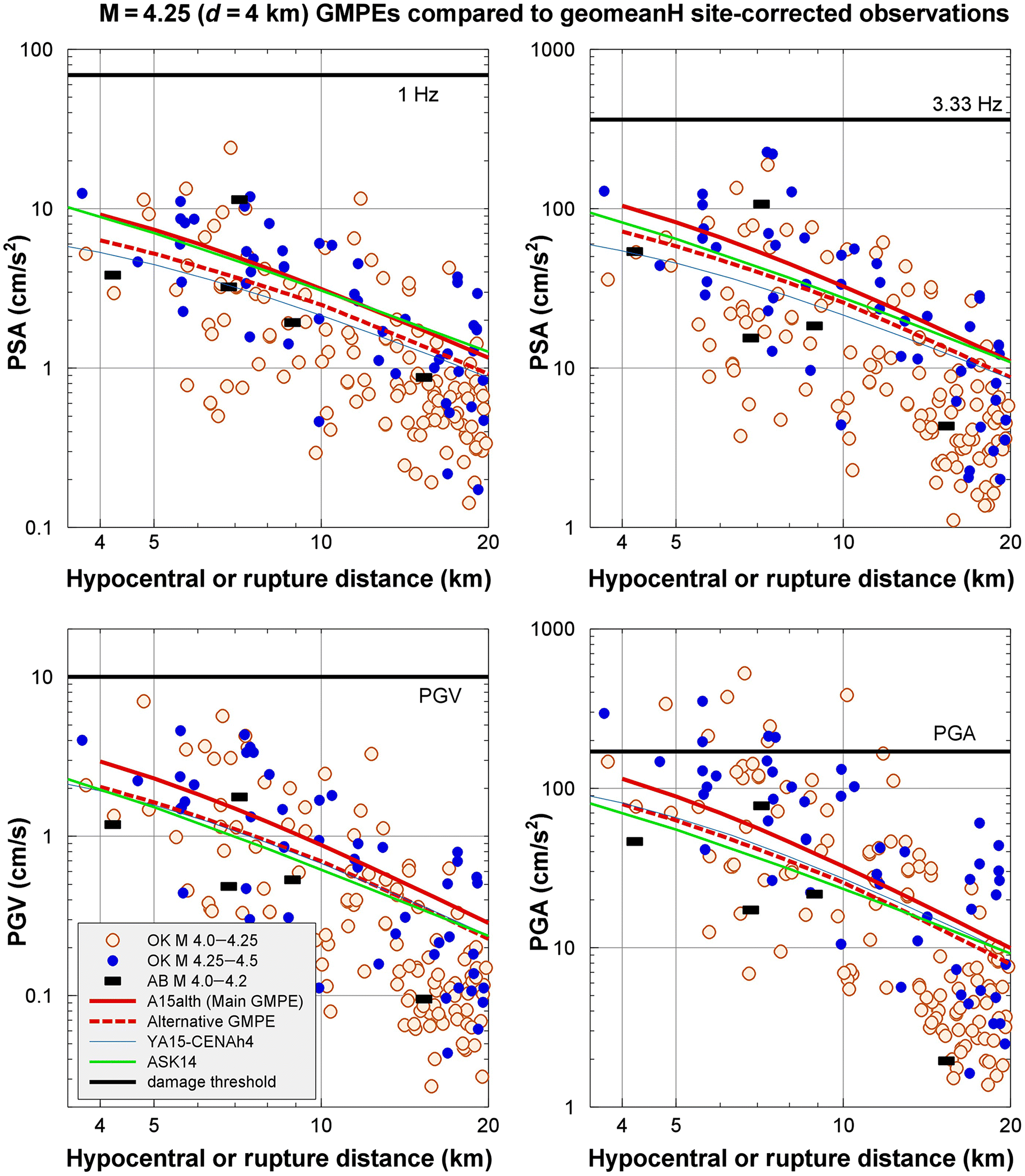
Of note in Fig. 5 is the high variability (scatter) of amplitudes about the median GMPEs. This is an important contributor to seismic hazard, as it means that ground motions are often significantly stronger than the median level, increasing the probability that a moderate event at close distance can cause strong ground motion. Another point of note is the level of observed ground motions for the magnitude range shown, M 4.0–4.5, relative to the damage threshold, which is taken as the motion that would typically result in a Modified Mercalli Intensity (MMI) of VI or greater. The ground motions corresponding to MMI = VI are estimated using the empirical relationships of Worden et al. (2012) between MMI and ground motion amplitudes. For high frequency ground motion parameters such as peak ground acceleration (PGA), the amplitudes for events of M ∼4 often exceed the damage threshold, whereas for lower frequency measures such exceedances will be less likely. This implies that the induced seismicity hazard is primarily a high frequency hazard, and thus, structures that are not sensitive to strong high frequency vibrations (i.e., long-period structures) would be less affected. The damage threshold is discussed in more detail later in the paper.
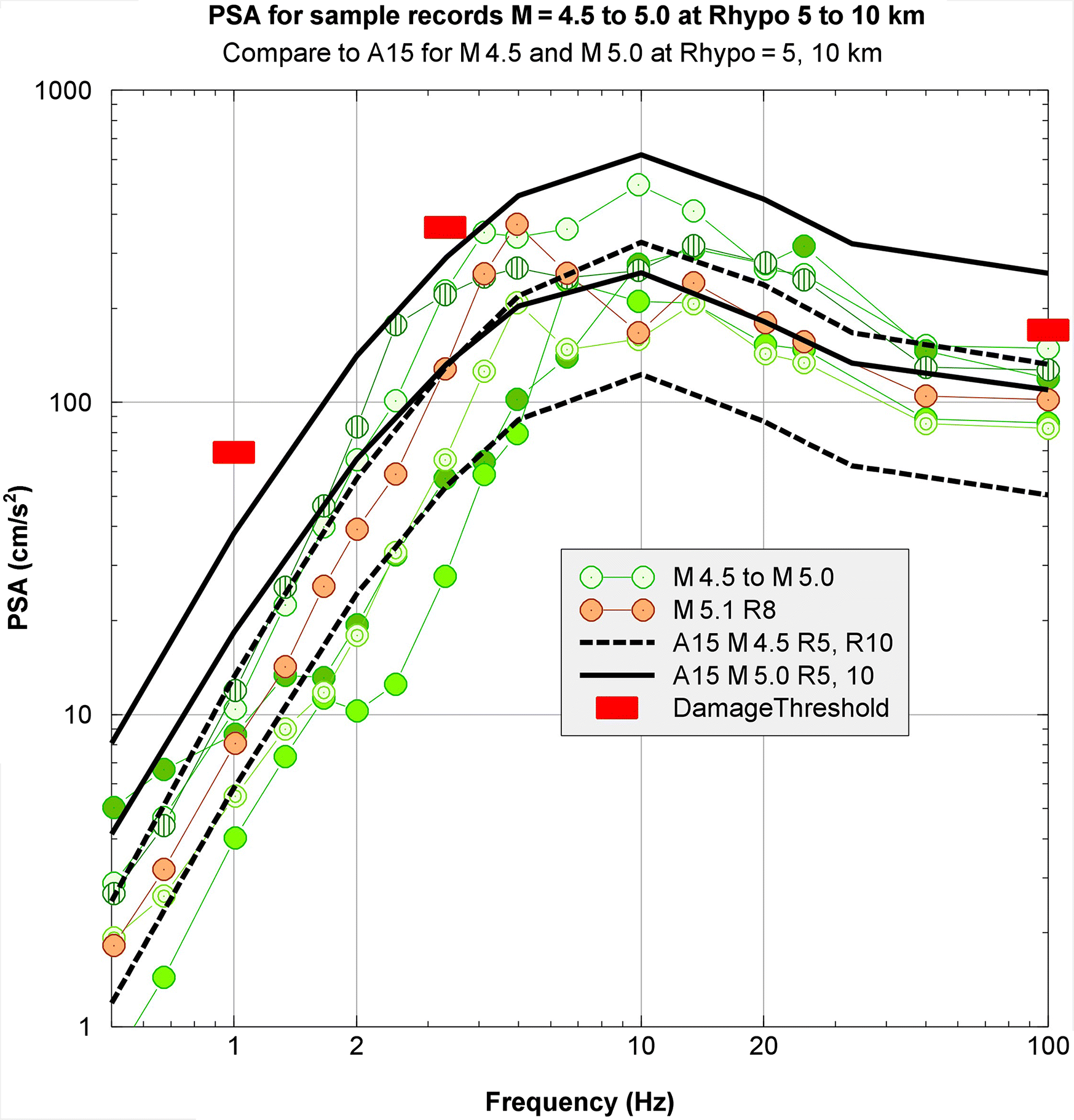
The frequency characteristics of typical induced events can be better appreciated by looking at plots of response spectra, which show the amplitude level versus vibration frequency for selected records. Figure 6 shows a sample of such records for induced events in Oklahoma of M 4.5–5.0 recorded in the hypocentral distance range from 5 to 10 km (corrected for site conditions, from Class C to B/C boundary). At high frequencies, the sample records tend to lie within the bounds that would be expected based on the Atkinson (2015) GMPE; they are slightly weaker than predicted at low frequencies. The ground motions that correspond to an MMI of VI, according to the relations of Worden et al. (2012), are also shown for this magnitude and distance range. This illustrates that these motions are near the damage threshold at high frequencies and below it for low frequencies.
Fig. 6.
Assessment and mitigation or avoidance of damaging ground motions
In this section, we consider the characteristics of induced events and their ground motions, with a view to developing strategies to reduce the likelihood of exceeding damaging ground-motion levels at a high-consequence site. This exercise can be considered in the context of the risk matrix approach of Walters et al. (2015), who considered green, yellow, and red zone classifications for operations that may induce seismicity, taking into account both the likelihood of damaging events and their potential consequences. In this context, operations very near to vulnerable high-consequence infrastructure can be considered in the red zone due to high exposure. Beyond the red zone, operations can be considered in the yellow zone, and at greater distances there would be a transition to the green zone. By analyzing the likelihood of damaging motions we can define red, yellow, and green zones for oil and gas operations using scientific risk-based principles.
We first define the ground motion characteristics that will be taken as having damage potential for vulnerable infrastructure. We then assess how to preclude the occurrence of those motions from a simple deterministic point of view, which is useful for illustrating concepts. Then, using a probabilistic approach we extend these ideas to the assessment and mitigation of potentially damaging ground motions; in this case, the goal is to ensure that the likelihood of potentially damaging motions does not exceed an acceptable value, such as 1/10 000 p.a. The approach taken here is generic, in that our ground motion index for assessment is the damage threshold based on MMI (as described below). For a specific application in which the definition of potentially damaging motions might be more refined, based on the structures at risk, the same approach could be refined accordingly. We could also refine the estimates of the likelihood of such motions for specific applications based on improved characterization of the site-specific hazard setting.
Characteristics of damaging ground motions
There is no single definitive measure of what makes ground-motion damaging. In general, the damage potential of ground motion depends on a combination of factors including amplitude, frequency content, and duration. Small-to-moderate events tend to be of short duration and are rich in high frequency content (at close distances), whereas larger events are longer in duration and have significant energy at longer periods. Moreover, the damage potential of motions will also depend greatly on the structural characteristics of the facilities in question, such as their overall robustness and frequency range of response. We can use MMI as a simple generic measure of damage potential that has a sound and well-calibrated empirical basis. In general, MMI = VI is the threshold for minor damage such as cracking to walls and chimneys. By comparison, MMI = III is the felt threshold, whereas MMI = VIII is the threshold for significant damage to well-engineered structures.
We can estimate ground motions that would typically result in MMI VI using empirical relations between ground motion amplitude and MMI. There are several such relations in the literature. For this exercise, the relations of Worden et al. (2012) were adopted, because they are based on a rich empirical database (from California) that explicitly includes the effects of amplitude, magnitude, and distance on MMI. It is important to realize that an inherent limitation of MMI is that it is a single number, whereas the underlying ground motion contains a range of amplitudes over an entire spectrum of frequencies. Thus, the relationship between MMI and ground motion varies with frequency; consequently, a single ground-motion record could be associated with a range of MMI values, with the most appropriate being either some average measure or possibly being dependent on the application (i.e., depending on whether high frequency or low frequency is of primary interest). Numerous authors have noted that, in general, PGA tends to be well correlated with felt effects (and lower MMI levels), whereas peak ground velocity (PGV) tends to be well correlated with damage (and higher MMI levels) (e.g., Worden et al. 2012). Worden et al. (2012) concluded that an optimal approach for estimating MMI from ground motion is to use the average value as predicted from PGA and PGV. Atkinson et al. (2014) followed this approach in their development of GMPEs for intensity in North America. This explains why MMI tends to be higher in the east than the west for the same magnitude of earthquake, even at close distances. The higher frequency content of eastern earthquakes and slower attenuation of high frequency motions within the competent eastern crust result in greater PGA compared with western events (whereas the PGV is similar) (e.g., Atkinson and Boore 2011).
The relations of Worden et al. (2012) predict that the median PGA associated with MMI = VI is 170 cm/s2 for moderate events at close distances (M ∼4.5 at ∼10 km). This intensity level is also associated with median response spectral amplitudes of 69 cm/s2 for PSA at 1 Hz and 363 cm/s2 for PSA at 3.33 Hz. These values are plotted as the damage threshold in Figs. 3–5. Note that these are median values, and there is significant variability in the amplitudes associated with MMI = VI (standard deviation of about a factor of two).
For PGV, the relations of Worden et al. (2012) predict that MMI = VI is associated with a median PGV = 9 cm/s. This is in good agreement with the range of values of PGV that are associated with damage potential based on blasting criteria and used to limit vibrations from quarry blasting and similar operations. For example, Westaway and Younger (2014) suggested a value of PGV = 5 cm/s for plaster cracking, with PGV = 6 cm/s being the damage threshold, whereas Siskind et al. (1980) suggested that damage to mortar or block foundations is associated with PGV = 12.7 cm/s. Considering this range of estimates, a value of PGV = 10 cm/s was adopted as the damage threshold for induced earthquakes.
Finally, a guide to the overall damage potential of a recorded ground motion can be obtained using the relations of Worden et al. (2012) to estimate the MMI associated with the PGA and PGV values (at the median level), then taking the average of these two estimates. If this average MMI value exceeds VI, we consider that the motion has damage potential. Whether damage would actually result depends on the characteristics of the structures at risk.
Simple deterministic approach
A conceptually simple approach to prevent damaging ground motions is to preclude events that could cause damage by specifying setbacks of operations from critical facilities—an exclusion zone within which operations will not occur. This ensures that earthquakes are not generated at very close distances. Such an approach requires the definition of a scenario event upon which to base the setback distance, which is a subjective exercise. If we consider hydraulic fracturing operations, Atkinson et al. (2016) estimated that ∼0.3% of HF wells will be associated with earthquakes of M ≥ 3. If we assume Gutenberg–Richter scaling with a typical slope of b = 1, it follows that the 1/10 000 event associated with completion of a HF well has a magnitude of M ∼4.5. We can calculate the PGA and PGV associated with an M = 4.5 event as a function of distance using GMPEs. Based on the discussion in the preceding sections, we take the geometric mean of the values predicted by the three GMPEs shown to be good proxies for induced events (Abrahamson et al. 2014; Atkinson 2015; Yenier and Atkinson 2015). The motions are evaluated at the median plus one standard deviation level; the use of the median plus sigma is a common practice in deterministic hazard assessments, to account for variability (e.g., Reiter 1990). Finally, the values of PGA and PGV are converted to MMI using the median relations of Worden et al. (2012); the averages of the PGA- and PGV-based MMI estimates are used to assess the expected MMI. This intensity is plotted as a function of distance from the hypocenter in Fig. 7.
Fig. 7.
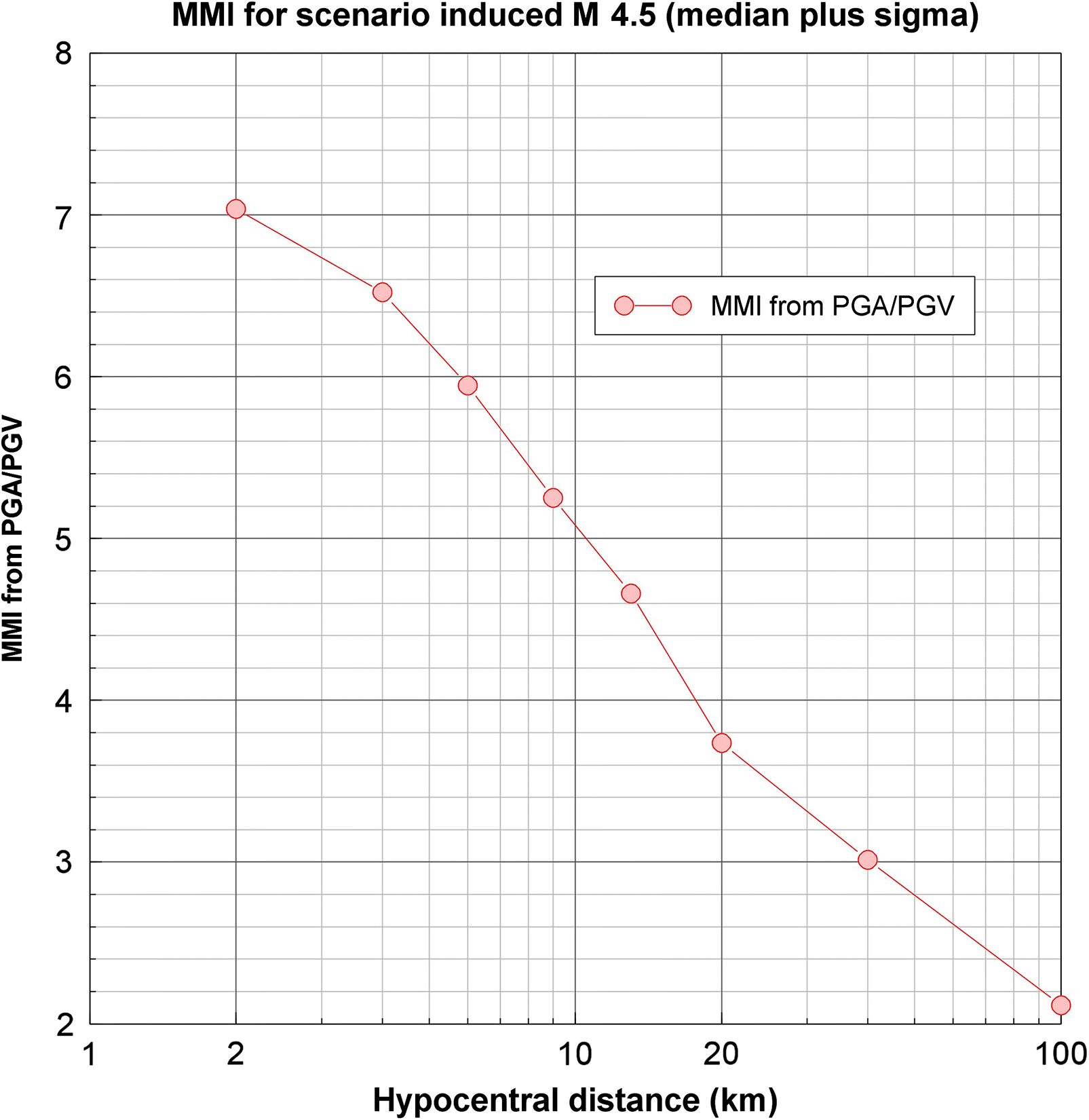
From Fig. 7, we conclude that events of M ∼4.5 are potentially damaging (MMI = VI) if they occur within a hypocentral distance of 6 km. If we assume that any triggered events would be initiated very close to the well, at a focal depth of ∼3 km we would require an exclusion distance for HF wells of 5 km laterally (i.e., in map view) for critical infrastructure to preclude potentially damaging motions. The appeal of a deterministic approach is its conceptual simplicity. However, it is limited by considering only a single magnitude level at a fixed sigma level, and that we have considered likelihood in only a very general way. The likelihood of the considered scenario is ∼1/10 000 (assuming an activation probability of 0.3%), but the total likelihood would, in reality, include other scenarios that we have not considered. It is thus difficult to assess whether or not the likelihood of potentially damaging motions is acceptable.
Probabilistic approach to assessment and mitigation or avoidance of ground motions
A more rigorous way to assess the ground motion hazard from induced events is to use a probabilistic approach, in which we can more readily consider the range of scenario events and their likelihoods and address their uncertainties. This is the aim of a classic PSHA. As described previously, the key inputs for a PSHA are the seismic source model, the recurrence statistics within seismic sources, and the GMPEs—along with the uncertainties and variabilities in these parameters. The use of the PSHA approach for induced seismicity applications was described by Atkinson et al. (2015a, 2015b). In this application, the model elements developed in the preceding sections are used to assess the induced seismicity hazard from hydraulic fracture operations in the area surrounding a site of interest. This facilitates the development of strategies that would limit the likelihood of potentially damaging ground motion to an acceptable level. For critical facilities, it is assumed that the maximum acceptable probability of potentially damaging motions (defined here as MMI = VI) is 1/10 000 p.a. Note that this considers only the induced seismicity hazard, whereas the total hazard is the sum of the induced and natural hazards. However, because the calculations carry a high level of uncertainty, this is a factor that is neglected for this exercise.
The PSHA is conducted using the Cornell–McGuire method for a source area that surrounds a site of interest, assuming that HF operations will be occurring at average regional rates for the WCSB (i.e., such as those over the last few years). The cellular rates of Ghofrani and Atkinson (2016), normalized for the area under consideration, are used to define the rate parameter (a value) of the Gutenberg–Richter relation for the source zone, as described previously. Specifically, a square source zone is defined that is 50 km × 50 km (2500 km2), with the site in the center. The rate of M ≥ 3 events for this square area is ∼0.075–0.25 p.a. for the assumed typical density of operations. The upper range of this rate is similar to that observed in the Fox Creek area, as noted previously. This rate (i.e., 0.25 M ≥ 3 p.a. in a box 50 km × 50 km) is adopted as the default for the calculations, assuming a b-value of 1.
The PSHA is conducted using the EQHaz software of Assatourians and Atkinson (2013). EQHaz conducts a Cornell–McGuire analysis based on a Monte Carlo approach, in which an earthquake catalog is simulated for the specified geometry and rate parameters of the source zones. Ground motions at the site are calculated for each event in the simulated catalog, drawing from a suite of GMPEs and their associated variability. The frequency statistics of the simulated ground-motion catalog define the hazard curves and can be used to explore their variability and uncertainty.
A minimum magnitude of 4.0 is assumed for the hazard calculations (see Atkinson et al. 2015b), meaning that only events above this magnitude will contribute to the calculated hazard. The maximum magnitude is assigned a distribution within the range of 5.0 to 6.5, using weights of 0.2, 0.3, and 0.5 for Mx = 5.0, 6.0, and 6.5, respectively. These values are slightly lower than those used in the national building code calculations for natural earthquakes in this region (Halchuk et al. 2014). The events are assumed to be distributed at depths from 3 to 6 km, using depth distributions of events of 2.0, 4.0, and 6.0 km with weights of 0.2, 0.5, and 0.3, respectively, and allowing a random 1 km perturbation in all depth values. The reader is referred to Assatourians and Atkinson (2013) for details of the hazard software and calculations; more details on hazard calculations for induced seismicity sources are given in Atkinson et al. (2015a, 2015b).
For the GMPE suite, the three candidate GMPEs discussed earlier (A15; YA15; ASK14) are used to define an uncertainty band around the A15 GMPE, as shown in Fig. 5; this is based on the representative suite approach (Atkinson and Adams 2013). The central GMPE is the A15 median GMPE, and a lower alternative is defined to represent the values suggested by alternative GMPEs. The lower alternative is defined by subtracting the value Δ, in log units, from the A15 GMPE, whereThis is a function that reduces the median amplitudes relative to A15 by 0.2 log units at very close distances, transitioning to a reduction of 0.1 log units at hypocentral distances (R hypo) of 10 km and greater. The A15 GMPE was convenient to use as the central GMPE because it is defined in terms of hypocentral distance. If larger events (>6.5) are considered, adjustments could be needed to accommodate potential saturation problems with this GMPE at large magnitudes. It is assumed that the standard deviation of ground motions about the GMPEs is 0.25 log units at low frequencies (and PGV), increasing to 0.3 log units at high frequencies (and PGA).
EQHaz is used to simulate catalogs of events and associated ground motions that would be expected if there are no exclusions on HF operations around the site. We can then examine this catalog to find what distance range of events needs to be precluded or controlled to ensure that the ground motions at the 1/10 000 p.a. level do not exceed MMI = VI. For this purpose, a synthetic catalog that is 1 000 000 years in length is generated. The ground motion having a probability of exceedance of 1/10 000 p.a. is the 100th largest amplitude in this catalog (i.e., 100 exceedances in 1 000 000 years are equivalent to an average exceedance rate of 1 in 10 000 years). Note that the catalog length is not intended to represent an actual duration of 1 000 000 years; rather, it can be thought of as 1 000 000 random realizations of a 1-year catalog of events. The large majority of these catalogs (>99%) will not result in a potentially damaging ground motion at the site, but rarely (<1% chance per annum), a large event will occur close to the site resulting in very strong ground motions.
Figure 8 shows the expected intensity (from the average values from PGV and PGA) at the site for the 1 000 000 year catalogue. It is observed that exceedances of MMI = VI come from moderate events at close distances, plus the rare possibility of larger events (M > 6) that would typically be at larger distances. The larger events are very rare (from the Gutenberg–Richter relation), so the odds of getting one very close to the site are very low. The total number of exceedances of MMI = VI (for the assumed cellular rate parameter of 0.03), with no exclusion zones, is >200, or more than double the target allowable number of 100 for 1/10 000 p.a. Figure 8 also shows the effect of an exclusion zone on the number of exceedances of MMI = VI. As we remove events within a certain distance range, by prescribing an exclusion zone about the site, the number of exceedances of MMI = VI will decrease, but the effect only becomes significant for exclusion distances of >5 km. The data in Fig. 8 suggest that if we are relying entirely on an exclusion zone to reduce the hazard, the exclusion distance would need to be ∼10 km to reduce the likelihood of potentially damaging motions to <1/10 000 p.a. This is greater than the deterministically derived exclusion distance of 5 km, because the probabilistic analysis indicates that there are significant hazard contributions from events of M > 4.5 at distances beyond 5 km.
Fig. 8.
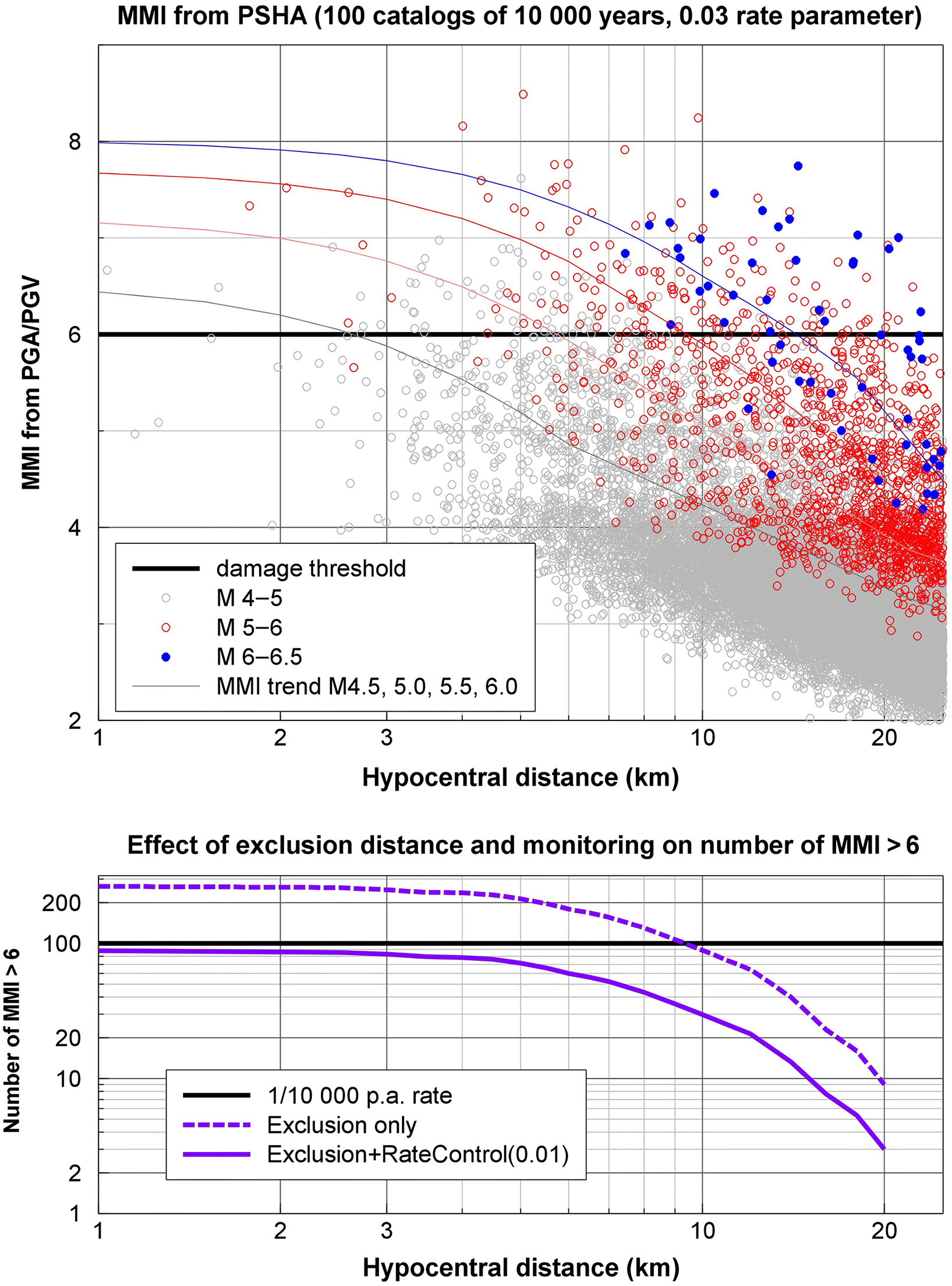
An alternative strategy to reduce the hazard is to combine an exclusion zone with a plan to ensure that the rate of induced events in the region, to a distance of ∼25 km, remains low—thus also reducing the likelihood of strong ground motions coming from more distant events. Figure 8 shows the effect of combining an exclusion zone with a stipulation that the cellular rate in the region, to 25 km, shall not exceed 0.01 p.a.; this has the effect of dividing the number of exceedances by a factor of 3 (from a rate of 0.03 to 0.01). From Fig. 8, we infer that the combination of an exclusion zone of 5 km laterally (6 km in hypocentral distance), plus a provision that the maximum cellular rate (for 10 km radius cell) be kept to <0.02 p.a. in the area extending out to 25 km, will achieve the objective of limiting the likelihood of potentially damaging motions to <1/10 000 p.a. The equivalent rate for the 25 km radius is a factor of 6.25 times greater (scaled for the larger radius), giving a maximum allowable rate parameter of 0.13 for M ≥ 3 or ∼1 event per annum for M ≥ 2 in the 25 km radius.
Finally, Fig. 8 shows that an overall control on the seismicity rate within 25 km could achieve the target probability without any exclusion zone. It may, therefore, be tempting to conclude that no exclusion zones for operations are required. However, such a conclusion would imply that there is no risk distinction between operations directly beneath a critical facility and those 20 km away. By contrast, common sense and an understanding of the scaling of ground motion with distance dictates that measures to avoid the potential for significant earthquakes should be focused preferentially on the near-distance range—especially considering the uncertainties in assessing the likelihood of such events. It is primarily the uncertainty in assessing the likelihood of triggering earthquakes, coupled with the high consequences of an error, which drive the cautionary logic behind an exclusion zone (i.e., the need to couple mitigation with avoidance).
Recommendations and conclusions
To avoid the potential for damage to critical infrastructure with very high failure consequences, the likelihood of damaging motions needs to be kept to <1/10 000 p.a. A two-pronged strategy that combines elements of avoidance and mitigation is effective in achieving this objective:An exclusion zone is required for situations in which the failure consequences would be unacceptable, because it is not possible to preclude the possibility that an HF well operation will be associated with seismicity at the M > 3 level—we do not have validated predictive models that allow such categorical determinations. This means that we cannot determine with sufficient confidence that the likelihood of damaging motions from such events is <1/10 000. In the risk matrix framework of Walters et al. (2015) this would be the equivalent of designating a red zone. Based on a simple deterministic analysis, an exclusion zone of 5 km is appropriate because that distance corresponds to the damage threshold for ground motions from events of M ∼4.5.
(i)
An exclusion zone with an approximately 5 km radius (in horizontal space) surrounding vulnerable high-consequence facilities.
(ii)
A monitoring and response protocol to ensure that the activity rates beyond the exclusion zone, to approximately 25 km, are kept below a specified limit.
A probabilistic hazard analysis shows that exclusion zones of less than 5 km are not effective in reducing hazard. The rate of damaging motions only begins to drop significantly for exclusion zones >4 km. However, a hazard analysis also shows that an exclusion zone alone is not sufficient to ensure that the induced event likelihood of damaging motions is <1/10 000 p.a., because much of the hazard comes from the possibility of moderate to large induced events (M > 5) beyond the exclusion zone. This hazard can be addressed by a monitoring and response protocol that is aimed at limiting the rate parameter for induced events in the region. This requires that events be monitored in real time within 25 km of critical facilities, and that we ensure the cellular rate parameter (for a 10 km radius cell) does not exceed 0.02 per annum for M ≥ 3. The equivalent rate for the 25 km radius is a factor of 6.25 times greater (scaled for the larger radius), giving a maximum allowable rate parameter of 0.13 for M ≥ 3 or ∼1 event per annum for M ≥ 2 in the 25 km radius. To meet this target, we need good monitoring within 25 km of critical facilities, coupled with a response protocol that will limit or adjust operations immediately if more than one event of M ≥ 2 is triggered within a year within the 25 km radius. In the risk matrix framework of Walters et al. (2015), the zone from 5 to 25 km would be considered the yellow zone, whereas the area beyond 25 km would be the green zone (at least from the point of view of the critical facility under consideration).
It should be noted that the implementation of an exclusion zone is an avoidance strategy, whereas the monitoring and response protocol is a mitigation strategy. An avoidance strategy is useful and appropriate for those few high-consequence facilities (such as major dams) where the target reliability level is very high and the failure consequences are unacceptable. However, avoidance may not be feasible for all structures, particularly those structures directly associated with the oil and gas operations themselves. For such structures, the focus would be on the use of seismically robust elements combined with an assessment, monitoring, and response protocol to reduce the likelihood of strong ground motions if required.
The analysis in this paper focused primarily on the hazard from hydraulic fracturing. A similar approach can also be taken for wastewater disposal wells, recognizing a few important differences. First, the area of impact of a disposal well is greater than that of a hydraulic fracture well, and thus, a larger exclusion zone may be warranted (i.e., perhaps of the order of 10 km). On the other hand, induced seismicity is likely to migrate relatively slowly away from a disposal well, in comparison with HF wells, and thus monitoring and response protocols may be more effective in tracking and reacting to induced events beyond the exclusion zone.
Finally, it is important to recognize the limitations of this study. The concepts outlined here are aimed at addressing the stringent reliability requirements that are mandated for high-consequence infrastructure. For such structures, avoidance strategies, in addition to mitigation strategies, are warranted. The same strategies may not be appropriate for typical structures, for which the target reliability is lower, and for which the repair of damage might be a feasible alternative strategy. Moreover, the specific strategies outlined here are based on limiting ground motions at an intensity level of MMI ≥ VI. This is appropriate for vulnerable structures. For modern robust structures with significant seismic resistance, the same principles could be used to relax the criteria required, particularly in the monitoring-and-response zone. However, it should be stressed that there is significant uncertainty in the computed probabilities of damaging ground motions, and this uncertainty is a major consideration, and cause for caution, in approaching hazard assessment and mitigation.
Acknowledgements
The author gratefully acknowledges the financial support of the Natural Sciences and Engineering Research Council of Canada, TransAlta, and Nanometrics, and extends thanks to Ryan Schultz and an anonymous reviewer for helpful comments and suggestions.
References
Abrahamson NA, Silva WJ, and Kamai R. 2014. Summary of the ASK14 ground motion relation for active crustal regions. Earthquake Spectra, 30: 1025–1055.
Assatourians K, and Atkinson G. 2013. EqHaz—an open-source probabilistic seismic hazard code based on the Monte Carlo simulation approach. Seismological Research Letters, 84: 516–524.
Atkinson G. 2015. Ground-motion prediction equation for small-to-moderate events at short hypocentral distances, with application to induced seismicity hazards. Bulletin of the Seismological Society of America, 105: 981.
Atkinson G, and Adams J. 2013. Ground motion prediction equations for application to the 2015 Canadian national seismic hazard maps. Canadian Journal of Civil Engineering, 40: 988–998.
Atkinson G, and Assatourians K. 2017. Are ground-motion models derived from natural events applicable to the estimation of expected motions for induced earthquakes? Seismological Research Letters, 88: 430–441.
Atkinson G, and Boore D. 2011. Modifications to existing ground-motion prediction equations in light of new data. Bulletin of the Seismological Society of America, 101: 1121–1135.
Atkinson G, and Martens S. 2007. Seismic hazard estimates for sites in the stable Canadian craton. Canadian Journal of Civil Engineering, 34: 1299–1311.
Atkinson G, Worden B, and Wald D. 2014. Intensity prediction equations for North America. Bulletin of the Seismological Society of America, 104: 3084–3093.
Atkinson G, Ghofrani H, and Assatourians K. 2015a. Impact of induced seismicity on the evaluation of seismic hazard: some preliminary considerations. Seismological Research Letters, 86: 1009–1021.
Atkinson G, Ghofrani H, and Assatourians K. 2015b. Impact of induced seismicity on the evaluation of seismic hazard. In Proceedings of the 11th Canadian Conference on Earthquake Engineering, Victoria, July 21–23, 2015, Paper 94365.
Atkinson G, Eaton D, Ghofrani H, Walker D, Cheadle B, Schultz R, et al. 2016. Hydraulic fracturing and seismicity in the Western Canada Sedimentary Basin. Seismological Research Letters, 87: 631–647
Bao X, and Eaton D. 2016. Fault activation by hydraulic fracturing in western Canada. Science, 17: aag2583.
Canadian Dam Association. 2007. Technical bulletin CDA-TB07 seismic hazard considerations [online]: Available from cda.ca/cda_new_en/regulations/regulations.html.
Canadian Dam Association Guidelines. 2013. Dam safety guidelines [online]: Available from imis100ca1.ca/cda/MainEN/Publications/Dam_Safety/MainEN/CDA/Publications_Pages/Dam_Safety.aspx.
Cornell C. 1968. Engineering seismic risk analysis. Bulletin of the Seismological Society of America, 58: 1583–1606.
Ellsworth W. 2013. Injection-induced earthquakes. Science, 341: 1225942.
Ghofrani H, and Atkinson G. 2016. A preliminary statistical model for hydraulic fracture-induced seismicity in the Western Canada Sedimentary Basin. Geophysical Research Letters, 43: 10164–10172.
Halchuk S, Allen T, Adams J, and Rogers G. 2014. Fifth generation seismic hazard model proposed to produce values for the 2015 National Building Code of Canada. Geoleological Survey of Canada. Open File 7576.
Keranen K, Savage H, Abers G, and Cochran E. 2013. Potentially induced earthquakes in Oklahoma, USA: links between wastewater injection and the 2011 Mw 5.7 earthquake sequence. Geology, 41: 699.
McGarr A. 2014. Maximum magnitude earthquakes induced by fluid injection. Journal of Geophysical Research, 119: 1008–1019.
McGuire R. 2004. Seismic hazard and risk analysis. EERI Monograph MNO-10. Earthquake Engineering Research Institute, Oakland, California.
National Research Council. 2013. Induced seismicity potential in energy technologies. National Academies Press, Washington, DC. [online]: Available from nap.edu/catalog/13355/induced-seismicity-potential-in-energy-technologies.
Petersen M, Frankel A, Harmsen S, Mueller C, Haller K, Wheeler R, et al. 2008. Documentation for the 2008 update of the United States National Seismic Hazard Maps: US Geological Survey. Open File Report 2008-1128. 61 p.
Petersen M, Mueller C, Moschetti M, Hoover S, Rubinstein J, Llenos A, et al. 2015. Incorporating induced seismicity in the 2014 United States National Seismic Hazard Model. Results of the 2014 workshop and sensitivity studies. US Geological Survey. Open File Report 2015-1070.
Reiter L. 1990. Earthquake hazard analysis; issues and insights. Columbia University Press, New York, New York.
Richter C. 1958. Elementary seismology. W.H. Freeman and Co., New York, New York.
Schultz R, Wang R, Gu Y, Haug K, and Atkinson G. 2017. A seismological overview of the induced earthquakes in the Duvernay play near Fox Creek, Alberta. Journal of Geophysical Research: Solid Earth, 122: 492–505.
Siskind DE, Stagg MS, Kopp JW, and Dowding CH. 1980, Structure response and damage produced by ground vibration from surface mine blasting. US Bureau of Mines. Report of Investigations 8507.
Van der Elst N, Page M, Weiser D, Goebel T, and Hosseini S. 2016. Induced earthquake magnitudes are as large as (statistically) expected. Journal of Geophysical Research: Solid Earth, 121: 4575–4590.
Walters R, Zoback M, Baker J, and Beroza G. 2015. Characterizing and responding to seismic risk associated with earthquakes potentially triggered by saltwater disposal and hydraulic fracturing. Seismological Research Letters, 86: 1110–1118.
Westaway R, and Younger P. 2014. Quantification of potential macroseismic effects of the induced seismicity that might result from hydraulic fracturing for shale gas exploitation in the UK. Quarterly Journal of Engineering Geology and Hydrogeology, 47: 333–350.
Worden B, Gerstenberger M, Rhoades D, and Wald D. 2012. Probabilistic relationships between ground motion parameters and Modified Mercalli Intensity in California. Bulletin of the Seismological Society of America, 102: 204–221.
Yenier E, and Atkinson G. 2015. Regionally adjustable generic ground‐motion prediction equation based on equivalent point‐source simulations: application to Central and Eastern North America. Bulletin of the Seismological Society of America, 105: 1989–2009.
Information & Authors
Information
Published In

FACETS
Volume 2 • Number 1 • January 2017
Pages: 374 - 394
Editor: Christoph E. Geiss
History
Received: 11 February 2017
Accepted: 14 March 2017
Version of record online: 27 April 2017
Copyright
© 2017 Atkinson. This work is licensed under a Creative Commons Attribution 4.0 International License (CC BY 4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Data Availability Statement
All relevant data are within the paper.
Key Words
Sections
Subjects
Authors
Author Contributions
All conceived and designed the study.
All performed the experiments/collected the data.
All analyzed and interpreted the data.
All contributed resources.
All drafted or revised the manuscript.
Competing Interests
The author has declared that no competing interests exist.
Metrics & Citations
Metrics
Other Metrics
Citations
Cite As
Gail M. Atkinson. 2017. Strategies to prevent damage to critical infrastructure due to induced seismicity. FACETS.
2(): 374-394. https://doi.org/10.1139/facets-2017-0013
Export Citations
If you have the appropriate software installed, you can download article citation data to the citation manager of your choice. Simply select your manager software from the list below and click Download.
Cited by
1. An Assessment of the Net Fluid Balance in the Alberta Basin
2. A Strategy for Choosing Red‐Light Thresholds to Manage Hydraulic Fracturing Induced Seismicity in North America
3. Mitigating injection-induced seismicity to reduce seismic risk
4. Intensity of Induced Earthquakes in Northeast British Columbia, Canada
5. Quantifying nuisance ground motion thresholds for induced earthquakes
6. Statistical Modeling and Characterization of Induced Seismicity Within the Western Canada Sedimentary Basin
7. Magnitude thresholds and spatial footprints of damage from induced earthquakes
8. The Intensity of Ground Motions from Induced Earthquakes with Implications for Damage Potential
9. Activation Rate of Seismicity for Hydraulic Fracture Wells in the Western Canada Sedimentary Basin
10. Risk-Informed Recommendations for Managing Hydraulic Fracturing–Induced Seismicity via Traffic Light Protocols
11. Hydraulic Fracturing‐Induced Seismicity
12. Developments in understanding seismicity triggered by hydraulic fracturing
13. Induced Seismicity
14. Ground Motion from M 1.5 to 3.8 Induced Earthquakes at Hypocentral Distance < 45 km in the Montney Play of Northeast British Columbia, Canada
