Assessment of soil organic carbon stocks in Alberta using 2-scale sampling and 3D predictive soil mapping
Abstract
A three-dimensional predictive soil mapping approach for predicting soil organic carbon (SOC) stocks (t/ha) at high spatial resolution (30 m) for Alberta for 2020–2021 is described. A remote sensing data stack was first prepared covering Alberta’s agricultural lands. A total of 404 sampling locations were distributed across Alberta using 2-scale sampling: (1) 22 pilot farms representing main climatic zones and (2) conditioned Latin hypercube sampling at each farm. Soil samples were taken at four standard depths (0–15, 15–30, 30–60, 60–100 cm) using soil probes and analyzed for SOC. Predictive models for SOC content and bulk density were built separately and then used to predict at 0, 15, 30, 60, and 100 cm and calculate aggregated SOC stocks per pixel. The SOC content and bulk density models had R squares of 0.61 and 0.68, respectively. Based on these mapping results, grassland soils were consistently associated with higher SOC stocks across all soil types as compared to croplands. The average SOC stock increase for grassland soils compared to cropland soils was 2.1 Mg per hectare, ranging from 2.17 to 6.09 Mg per hectare depending on soil type. Results also showed that >15 % of total SOC stocks were located in subsoil, which was higher than expected.
1. Introduction
Soil organic carbon (SOC) is an essential part of the global carbon cycle, with the pedosphere containing 4.5 times more carbon than in vegetation (Lal 2022). Despite the importance of SOC, there is still much uncertainty regarding how much agricultural soils could sequester SOC from the atmosphere (Lal et al. 2018; Tifafi et al. 2018). Global SOC stock estimates vary widely with values ranging from 500 to 3000 Pg, with a median estimate of 1500 Pg (Scharlemann et al. 2014; Tifafi et al. 2018). Bai and Cotrufo (2022) estimated that there is an achievable SOC sequestration potential in global grasslands of 2.3–7.3 billion tons of carbon dioxide equivalents per year (CO2e year−1). Given the wide ranges and high uncertainties of how much SOC there is and what the SOC sequestration potential may be, there is a need to refine estimates of SOC stocks, particularly at finer spatial scales.
The agricultural region of the Canadian Province of Alberta covers approximately 258 000 km2 and currently lacks detailed SOC maps to support SOC monitoring projects (KC et al. 2021). Grassland soils in Alberta are an important carbon store. Global grassland SOC stocks are estimated at 343 Pg in the top 1 m, which is higher than forest carbon stocks (Conant et al. 2017). Proportion of SOC stocks in the top 20 cm varies by land use type, with 42% of SOC stock in the top 20 cm in grassland soils compared to 50% for forest soils (Jobbagy and Jackson 2000; Lal 2022). Conversion of crop to pasture land has been documented to increase SOC stocks, with conversion from pasture to crop leading to a loss of SOC (Guo and Gifford 2002; Lal 2022). However, globally, there continues to be a conversion of grazing lands to cultivated crops (Ramankutty et al. 2008). As grasslands represent an important store of SOC, improved mapping of grassland and cropland SOC stocks is essential for improving carbon estimates and understanding the effects of land use change on carbon budgets (KC et al. 2021).
Predictive soil mapping is a tool that can help researchers and land managers better understand variation of SOC stocks as a function of soil properties and land use. Predictive soil mapping has increasingly emerged as a technique to improve understanding of spatial variation of soil properties (Ellili et al. 2019; Hengl and MacMillan 2019). Mapping of SOC content has been completed at a global scale at 250 m (Hengl et al. 2017; Poggio et al. 2021). Guevara et al. (2020) have also mapped SOC content at 250 m across Mexico and the Conterminous United States. Recently, a finer scale SOC content map for Canada was generated at 250 m by Sothe et al. (2022), which is currently the state-of-the-art SOC content map of Canada to date.
Given the importance of SOC, and grassland SOC particularly, and still relatively high uncertainty surrounding SOC stock estimates, we focused on mapping SOC stocks across Alberta’s agricultural region using newly collected soil samples with consistent measurements. Our main research objectives were to
1.
produce a high spatial resolution map of the SOC stock distribution for agricultural land in Alberta,
2.
examine the effect of using more prairie and grassland specific training data in terms of SOC stock estimates,
3.
compare grassland versus cropland SOC stocks among different soil types across Alberta’s agricultural region, and
4.
determine the baseline SOC stocks for cropland and grassland soils across Alberta’s agriculture region.
2. Data and methods
2.1. Soil samples and observations
We used two soil data sets for training the predictive soil mapping models. The first soil data set was a legacy data set: The Assessment of Environmental Sustainability in Alberta’s Agricultural Watersheds Project (AESA) Soil Quality Monitoring Project from 1997 to 2001 (Cathcart et al. 2008). This data set consists of 291 soil samples from 44 sites across a range of Alberta agricultural soils with SOC and bulk density measurements. AESA can be considered a legacy soil data set for monitoring SOC changes across Alberta.
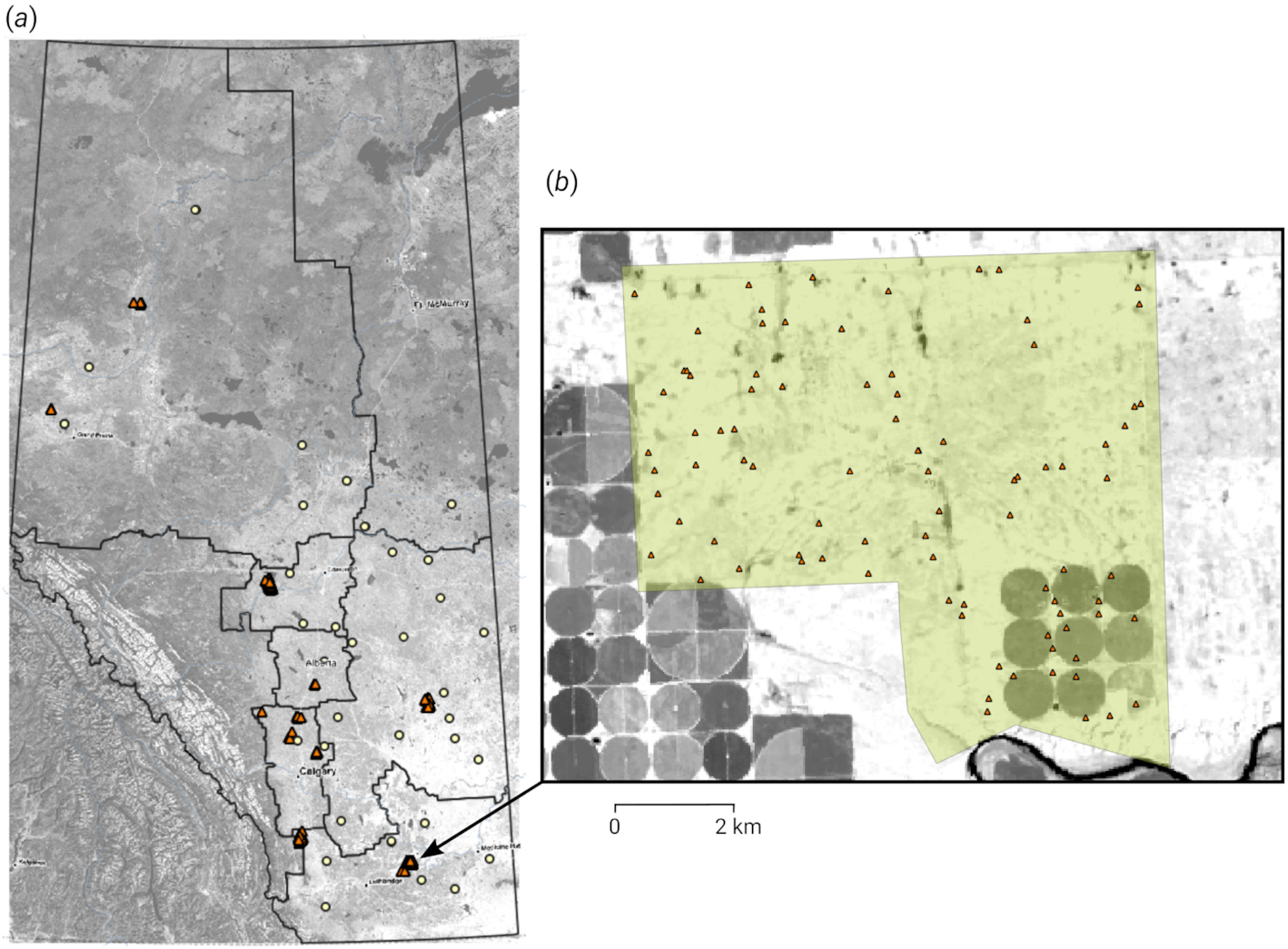
The second soil data set (404 sites; 1491 samples), i.e. new data, was collected specifically for this project using a predefined soil carbon sampling approach. Due to budget limitations and the size of Alberta, instead of trying to recreate probability sampling across the entire agricultural region of the province, we used a 2-phase spatial sampling to maximize the spread of sample locations and minimize the costs: (1) in the first phase, we used climate, terrain, and lithological parameters to identify 10 farms across an environmental gradient, and (2) in the second phase, we allocated sampling sites within each farm using consistent sampling intensity and conditioned Latin hypercube sampling (Minasny and McBratney 2006; Brus 2021) as implemented in the clhs package in R (Roudier et al. 2012; Roudier 2021) and described in detail at https://opengeohub.github.io/spatial-sampling-ml/. It is important to note that the 10 farms were selected based on climate, terrain, and lithological parameters using tacit knowledge, and potential locations were limited by existing landowner relationships. Therefore, the entire feature space may not be adequately covered and future modeling efforts with more data can improve the mapping results.
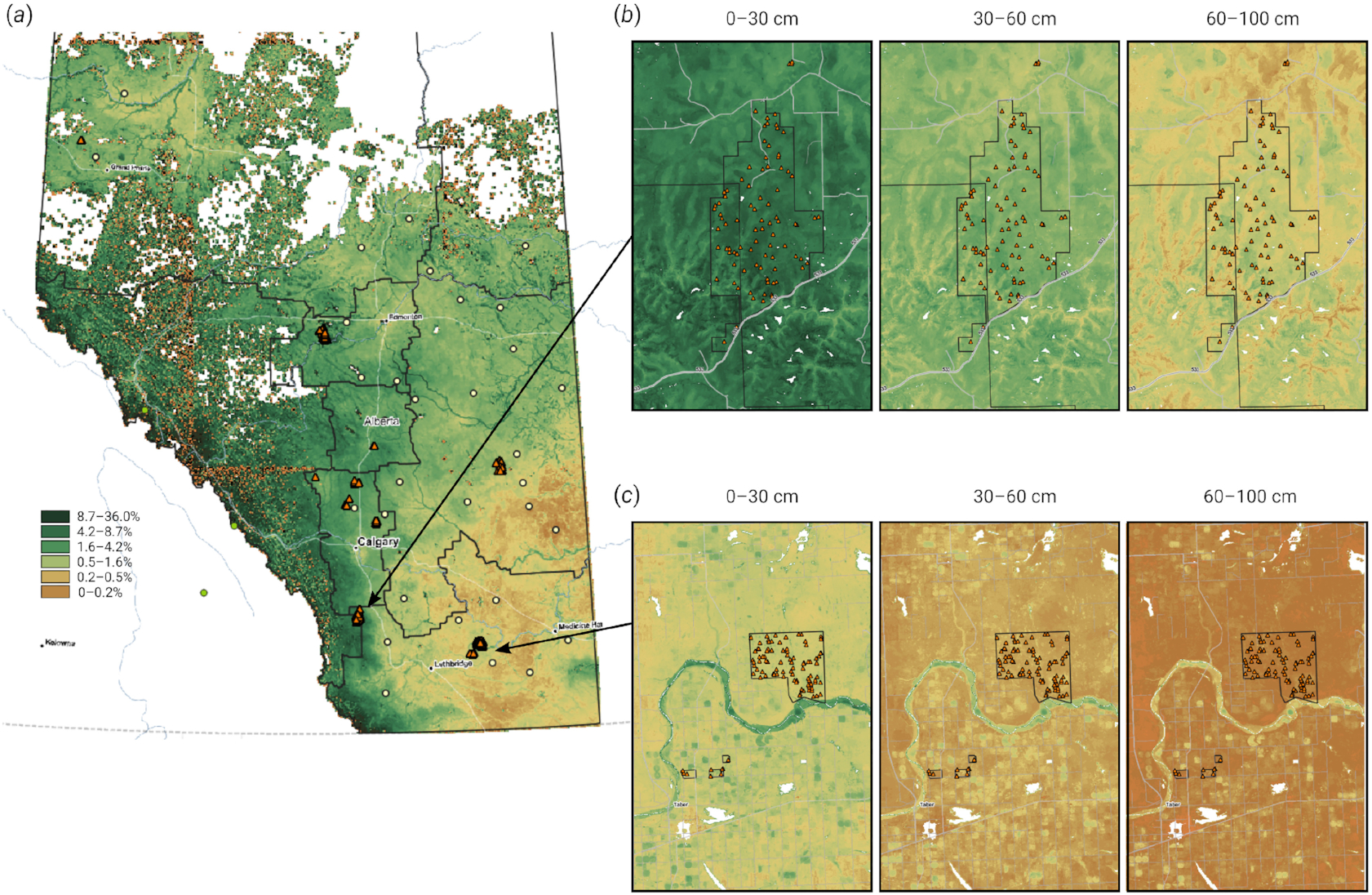
Fieldwork for this dataset was conducted in 2019 and 2020 following a consistent sampling protocol using mechanized soil probes. At each location, a soil sample core was collected and broken into to the following standard depth increments: 0–15, 15–30, 30–60, and 60–100 cm. Samples from each increment were then analyzed for SOC content by dry combustion (Nelson and Sommers 1983; Roper et al. 2019) using a Carlo Erba NA 2100 Elemental Analyzer (Carbo Erba Strumentazione, Milan, Italy). Bulk density and coarse fragment content were also determined during laboratory analysis. The sampling locations across Alberta are illustrated in Fig. 1.
Fig. 1.
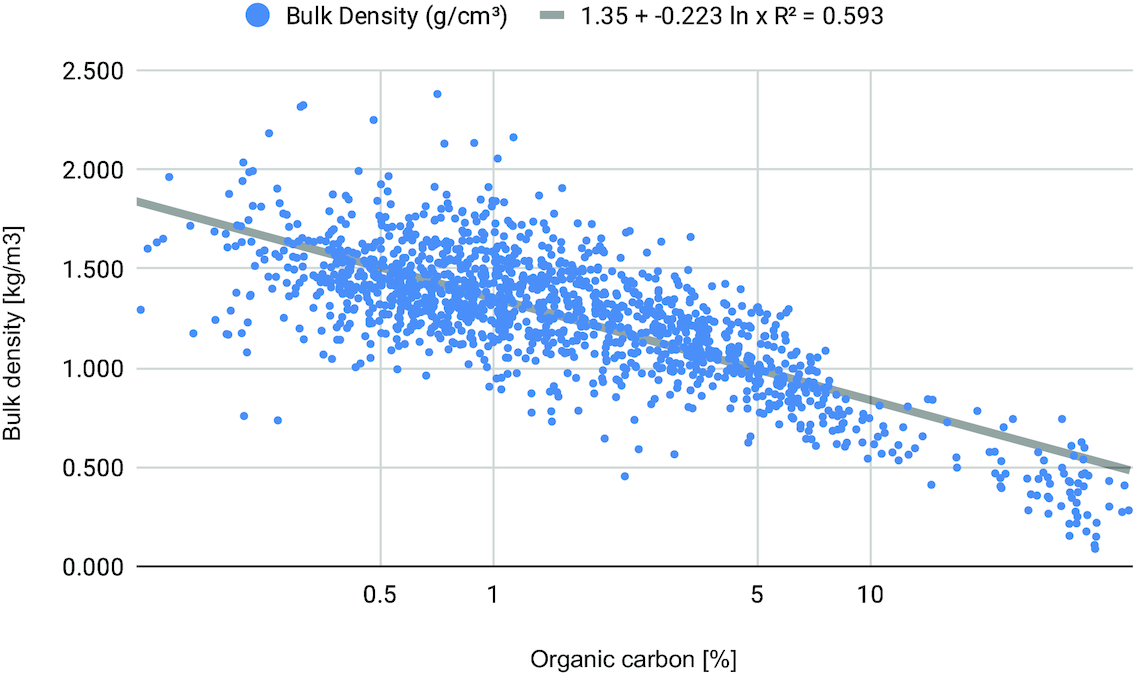
After laboratory analyses and data entry, all points were inspected for possible artifacts and gross errors. This was done by producing two-dimensional (2D) scatter and multivariate plots to detect potential outliers. Bulk density was available for a majority of soil samples. The remaining 10% of samples with missing values were estimated used a pedotransfer function shown in Fig. 2 fitted locally using the AESA dataset.
Fig. 2.
Because the AESA SOC data were determined using loss on ignition and not dry combustion, we harmonized the loss-on-ignition values to avoid any bias in estimates (Roper et al. 2019). For this we used the formula provided by Jensen et al. (2018) that accounts for the clay content of soil:where SOC is soil organic carbon content, LOI is soil organic carbon loss-on-ignition values, and CLAY is clay content.
(1)
2.2. Covariate layers
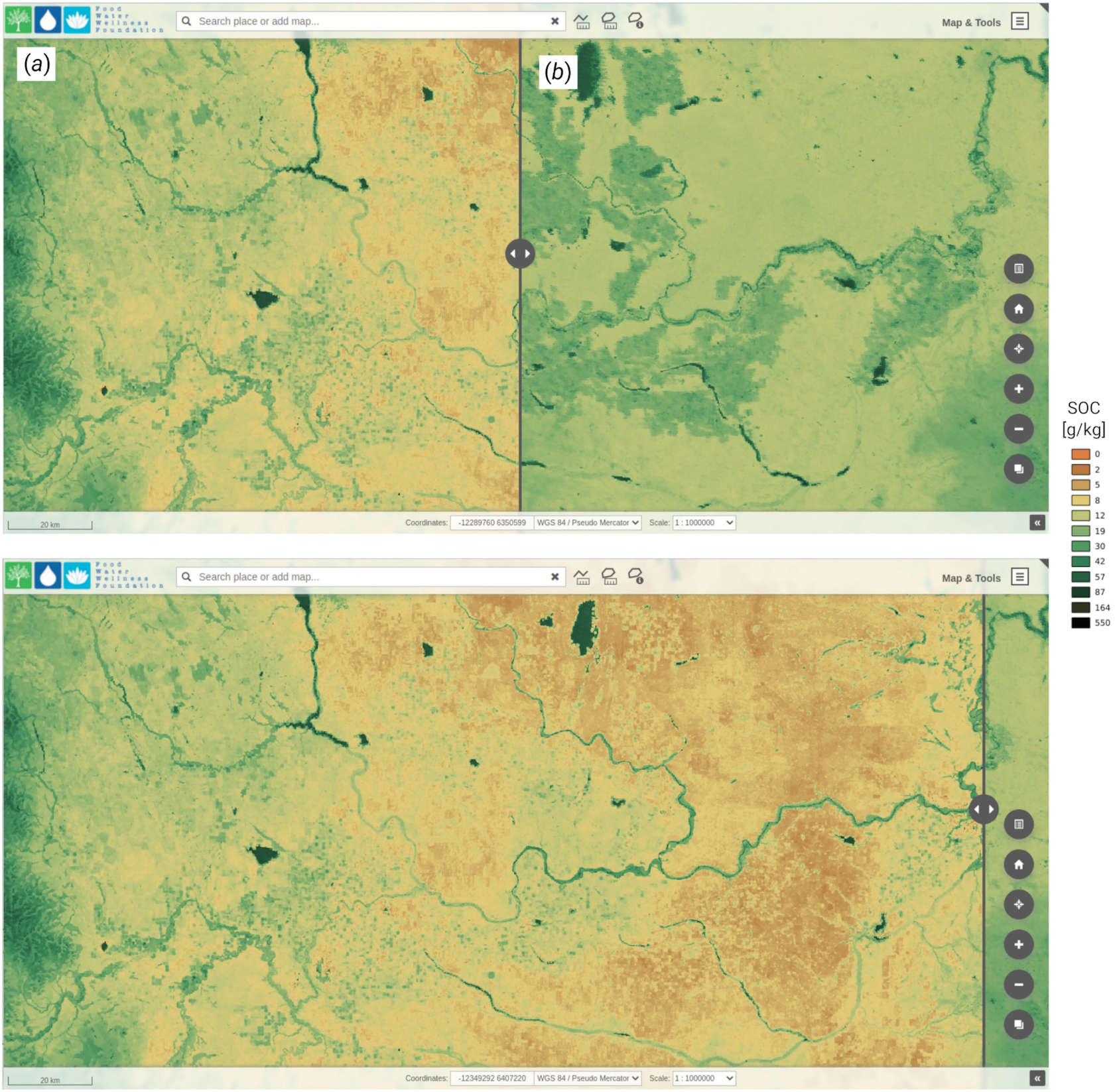
We focused on mapping SOC at spatial resolutions finer than recent Canada-wide work (Sothe et al. 2022); hence, we prepared the covariate layers at spatial resolutions of 30 m. We prepared 180 covariates that can be grouped roughly into four themes:
•
Climate: we used ClimateNA v7.3 normals for 1990–2010 at 1 km spatial resolution (Mahony et al. 2022), which were obtained from https://adaptwest.databasin.org/pages/adaptwest-climatena/ and then downscaled using cubic splines for prediction purposes.
•
Relief: we used the Advanced Land Observation Satellite (ALOS) Digital Terrain Model (DTM) of Alberta at 30 m (Jaxa 2015).Terrain derivatives including standard morphometric and hydrological parameters at 30, 100, and 250 m spatial resolution were determined (Behrens et al. 2018).
•
Organisms: we used the Moderate Resolution Imaging Spectroradiometer (MODIS) Enhanced Vegetation Index (EVI) long-term composites, PROBA-V Level3 Normalized Difference Vegetation Index (NDVI) (Wolters et al. 2014) long-term monthly estimates, and Landsat Analysis Ready Data (ARD) 25th Percentile (P25), 50th Percentile (P50), and 75th Percentile (P75) images for spring and summer months (Potapov et al. 2020; Witjes et al. 2022).
•
Parent material: we prepared lithological units for Alberta based on the Bedrock Topography of Alberta Version 2 (Alberta Geological Survey 2020) downloaded from https://ags.aer.ca/data-maps-models/data/dig-2020-0022; the units were converted to indicator maps for (1) colluvial deposits, (2) eolian deposits, (3) fluvial deposits, (4) glaciofluvial deposits, (5) glaciers, (6) lacustrine deposits, (7) glaciolacustrine deposits, (8) moraine, (9) fluted moraine, (10) stagnant ice moraine, (11) ice-thrust moraine, (12) organic deposits, (13) bedrock, and (14) preglacial fluvial deposits.
Preparation of the PROBA-V and Landsat long-term composites for recent years (2018–2020) required downloading the images from the GLAD Landsat ARD Tools (https://glad.umd.edu/ard/) and then downloading long-term composites for four seasons (winter, spring, summer, and autumn months), removing snow cover and gap filling all missing pixels. The 7-band Landsat images produced a total of 168 GeoTIFFs (4 seasons × 3 percentiles × 7 bands × 2 years) that were then used as covariate layers. Detailed processing steps used to derive Landsat derivatives are available in Witjes et al. (2022).
The rationale for using Landsat time-series composites for soil property mapping was as follows: although Landsat images do not penetrate soil and primarily reflect above ground vegetation (hence can not be used to measure SOC directly), we believe that by having full multi-year seasonal composites with three percentiles we can find key correlations among soil properties and the temporal signature of a pixel. Single-satellite images of a field can be strongly affected by crop-rotation effects, which are then reflected on predictions of soil properties. These crop-rotation effects most likely do not have anything to do with changes in soil properties, as many cropping systems’ above ground vegetation changes seasonally and abruptly with exactly the same soil properties. It is also important to emphasize that as data were used within a Machine Learning framework, primarily by fitting complex decision trees (e.g. Random Forest), each combination of crop rotation, seasonality, and other relationships that best fit the training data were determined. This assumption has worked in previous case studies (Hengl et al. 2021, 2022a), with predictions not reflecting crop boundaries or similar patterns.
Although finer resolution spectral bands are now available, primarily thanks to the Sentinel-2 mission (up to 10 m spatial resolution), we focused on using Landsat as the key earth observation (EO) data for soil property mapping because our interest is the use of EO data to reconstruct historical SOC dynamics going back 10, 20, and 30 years.
After we prepared all covariate layers, training points were overlaid with 250 and 100 m resolution layers (climatic layers, MODIS LST, geological classes) and 30 m resolution layers (Landsat GLAD percentiles for bands for 2019 and 2020 digital terrain parameters) and then combined to produce a regression matrix with all covariate layers and target variables at different soil depths.
The whole of Alberta at 30 m as mosaics are images of 23 144 columns by 41 125 rows in the EPSG:3402–NAD83(CSRS)/Alberta 10-TM (Forest) coordinate system. The total data prepared for SOC mapping exceeded 200 GB. This means that a significant infrastructure is needed to process these data. Predictions were the most time-consuming task in the total workflow and were run in a high-performance computing environment (Intel Xeon Gold 6284R with 96 threads and 378 GB RAM) to avoid RAM limitations and delays.
2.3. 3D Ensemble Machine Learning
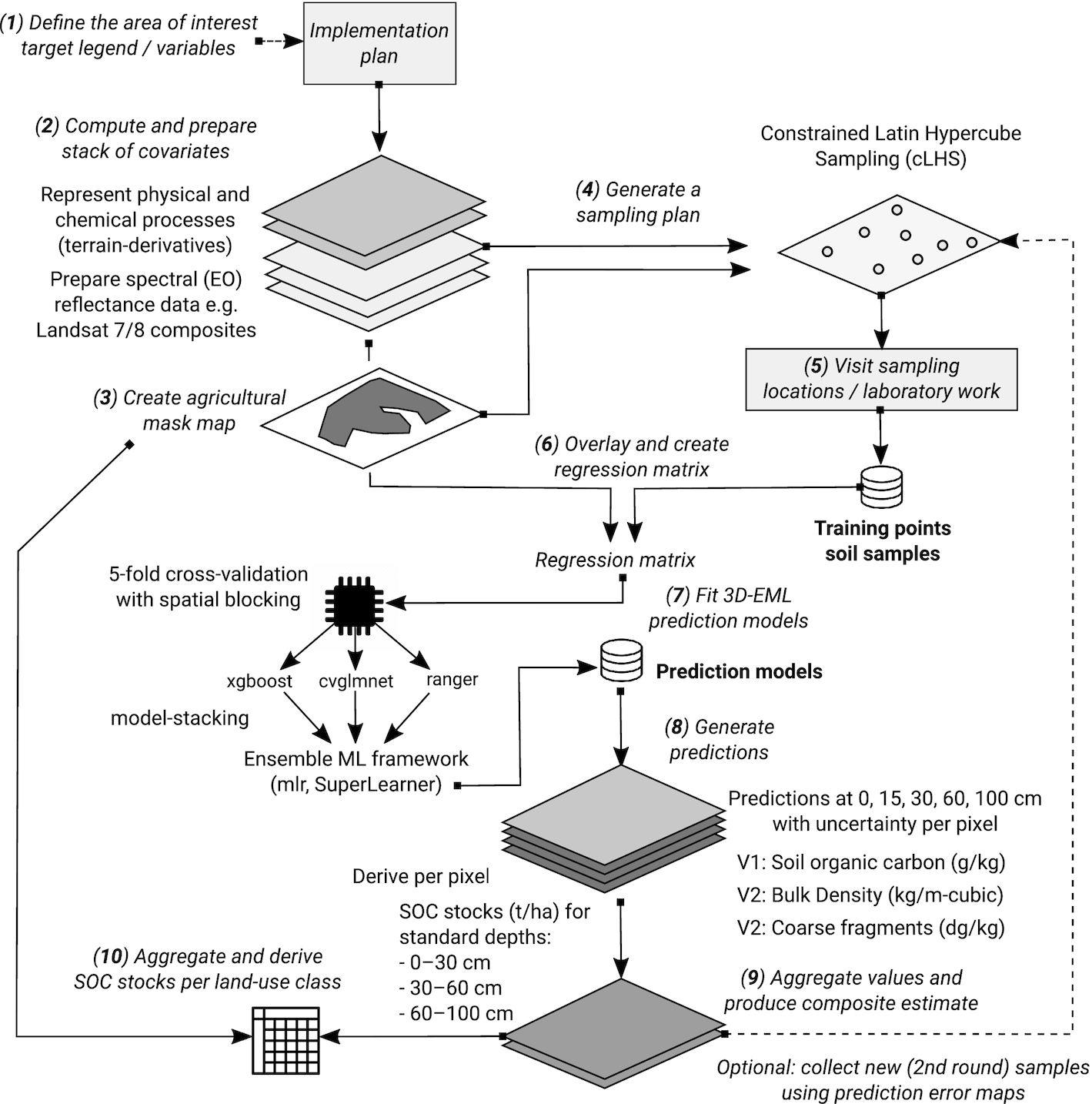
We used a three-dimensional (3D) Ensemble Machine Learning (3D-EML) framework to model spatial distribution in SOC and soil bulk density as explained in Fig. 3. We first defined an area of interest (agricultural mask) and prepared a list of covariate layers representing soil-forming factors (steps 1–3). We then used the covariate layers to design a sampling design (step 4) based on conditioned Latin hypercube sampling to ensure unbiased representation and minimal extrapolation space within the sampled farms (Brus 2021). We next collected samples on the ground and carried out consistent laboratory analysis (step 5). The data from the samples were then quality-controlled and overlaid with covariate layers and used to build predictive models (steps 6–7) to map SOC content and bulk density independently (step 8).
Fig. 3.
After we produced predictions of SOC content and bulk density at depths 0, 15, 30, 60, and 100 cm, we derived aggregate estimates of the SOC stocks in depth increments of 0–30 cm (top-soil), 30–60 cm (sub-soil1), and 60–100 cm (sub-soil2) (step 9). The depth-wise estimates were modeled using a threshold as described in Hengl and MacMillan (2019), where the values for the 0–30 cm depth interval were split into two values at 0 and 30 cm. These estimates were then crossed with the land use and soil type maps for Alberta to produce summaries per combination of classes.
The 3D-EML approach incorporated soil depth as a covariate, which enabled the prediction of a given soil parameter at any depth. The advantage of this approach over mapping each depth independently was that the total training data set could be maximized and variations in depth profiles could be accounted for in the model (Hengl and MacMillan 2019; Hengl et al. 2021). A disadvantage of this approach was that only the depth variable was modified and values of covariates at various depths were considered to be constant, which was a gross assumption. Ma et al. (2021) compared the 3D predictive soil mapping with 2D approaches, including a combination with spline fitting of soil horizons and showed that 3D mapping produced comparable accuracy and was easier to implement as compared to 2D approaches that include multiple additional steps such as spline fitting/gap filling.
Ensemble predictions were based on stacking three independently fitted models (Hengl et al. 2022a):
1.
ranger: fully scalable implementation of Random Forest (Wright and Ziegler 2017),
2.
XGboost: extreme gradient boosting (Chen and Guestrin 2016), and
3.
glmnet: GLM with Lasso or Elasticnet Regularization (Friedman et al. 2020).
We ran model fitting and prediction in four phases, as implemented in the mlr framework for Machine Learning in R (Bischl et al. 2016). Standard four modeling steps included
1.
Hyper-parameters fine-tuning: we first determined mtry for ranger and XGBoost parameters by iterative fine-tuning;
2.
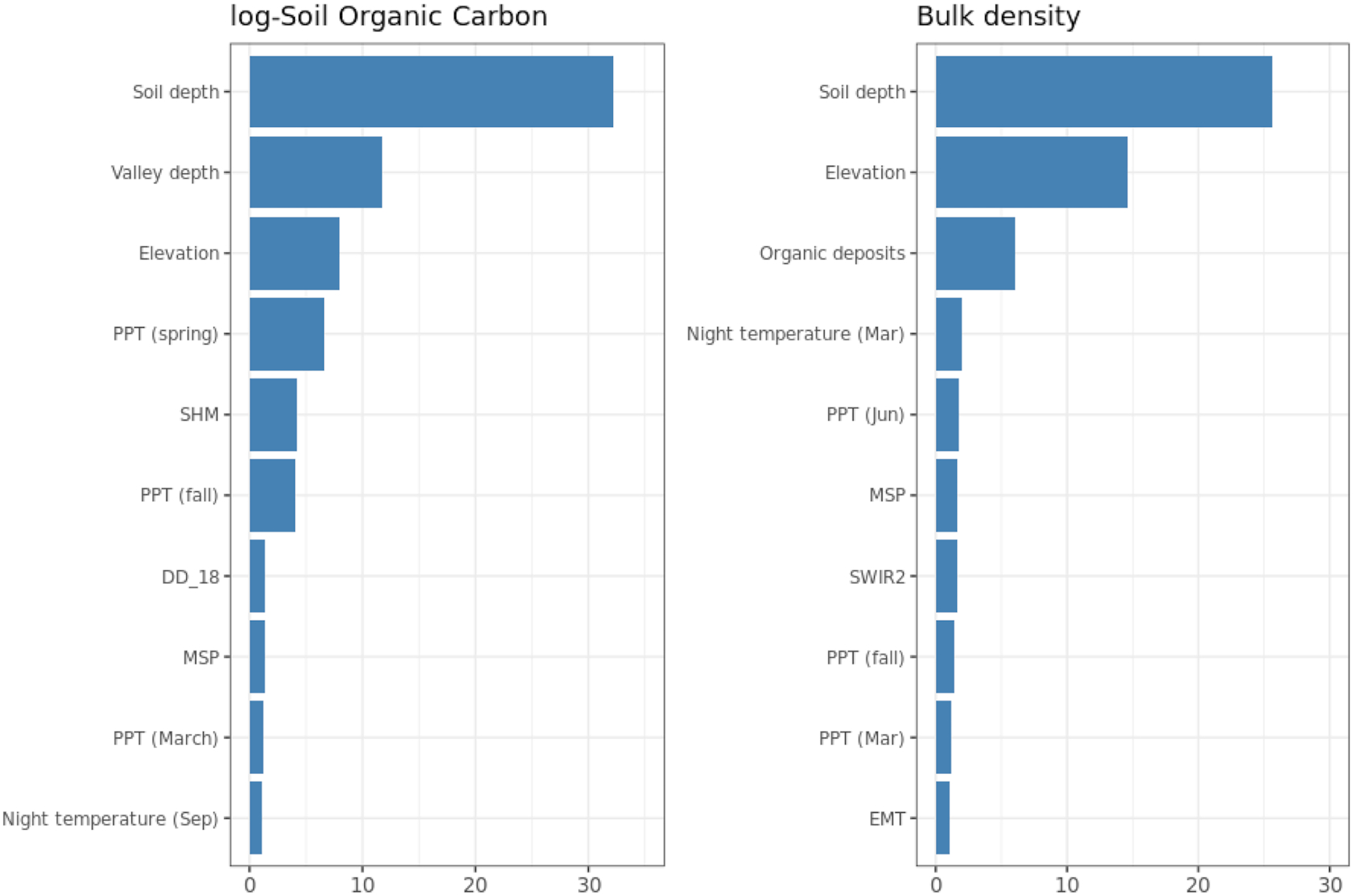
Feature selection: we subset covariates using random feature selection in mlr, which usually removes 30%–40% of covariates;
3.
Stacking: we used 5-fold cross-validation with spatial blocking (5 × 5 km) to generate a meta-learner;
4.
After the model fitting, we produced predictions and estimated the prediction errors (per pixel) by first fitting a quantile regression RF model using three learners and then derived root mean square percentage error per pixel using the forestError package (Lu and Hardin 2021).
We used EML rather than a single learner (e.g. Random Forest) for two main reasons: (1) it is a remedy for potential over-fitting and (2) in the case of variables with skewed distributions, it helps reduce overshooting effects (Hengl et al. 2022a, 2022b). In the case of spatially clustered samples (this study also), spatial blocking (i.e. spatial cross-validation) during model training helped reduce potential over-fitting that can be significant (Gasch et al. 2015; Schratz et al. 2019). When points are based on probability sampling and regularly distributed across areas of interest, spatial cross-validation has produced over-pessimistic estimates of mapping accuracy (Wadoux et al. 2021). In our case, because sampling points were clustered around selected farms, we needed to use spatial blocking (with 30 km tiles) during model training to prevent overfitting. Also, we assumed that to get a realistic estimate of the mapping accuracy for the whole of Alberta, we removed whole farms from training/validation.
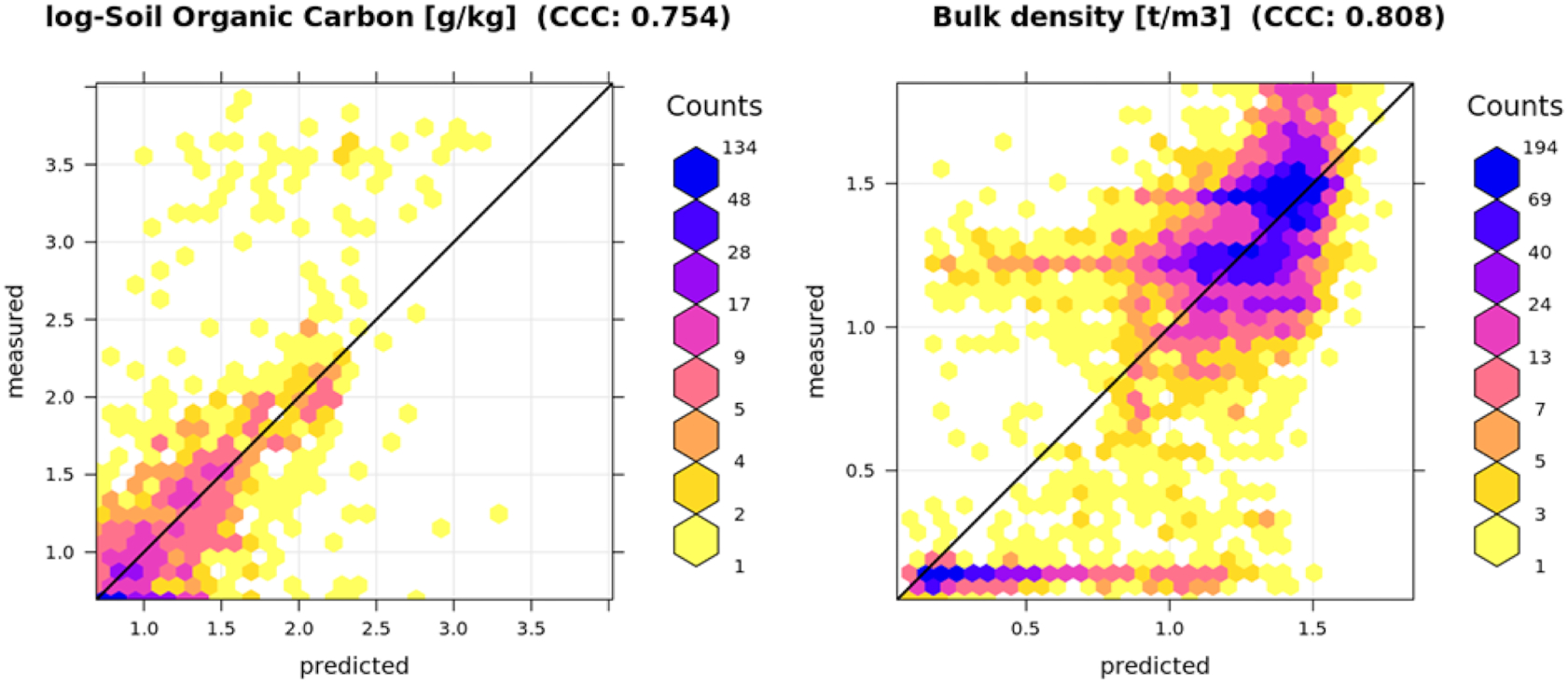
Note also that we modeled the log-transformed variable for SOC and coarse fragments (both follow log-normal distribution) and then back-transformed after modeling. The rationale to work with the log-transformed variable is as follows: first, by log-transforming the target variable, we reduced the effect of very large SOC concentrations (e.g. high SOC in wetlands and similar areas that might result in low values being over-estimated); secondly, for the log-transformed variable, which then showed close to normal distribution, it was easier to interpret the root mean square error (RMSE) and visualize results.
2.4. Derivation of soil carbon stocks
Our main objective was to map SOC stocks in t/ha and not only SOC content. In principle, in predictive soil mapping, there are three main ways to derive SOC stocks from soil samples (Hengl and MacMillan 2019):
1.
The 2D approach: estimate SOC stocks in t/ha for fixed depths, e.g., 0–30 cm, and then model and predict stocks or estimate SOC content and bulk density for each depth separately and combine to estimate total SOC stock.
2.
The 3D uni-variate approach: estimate SOC density in kg/m3 for each soil depth (training samples) and then predict in 3D and aggregate to standard depth intervals (Sanderman et al. 2018).
3.
The 3D multivariate approach: model and predict SOC content (g/kg), bulk density (kg/m3), and coarse fragments (dg/kg) independently in 3D and then aggregate to standard depth intervals and derive SOC stocks in t/ha.
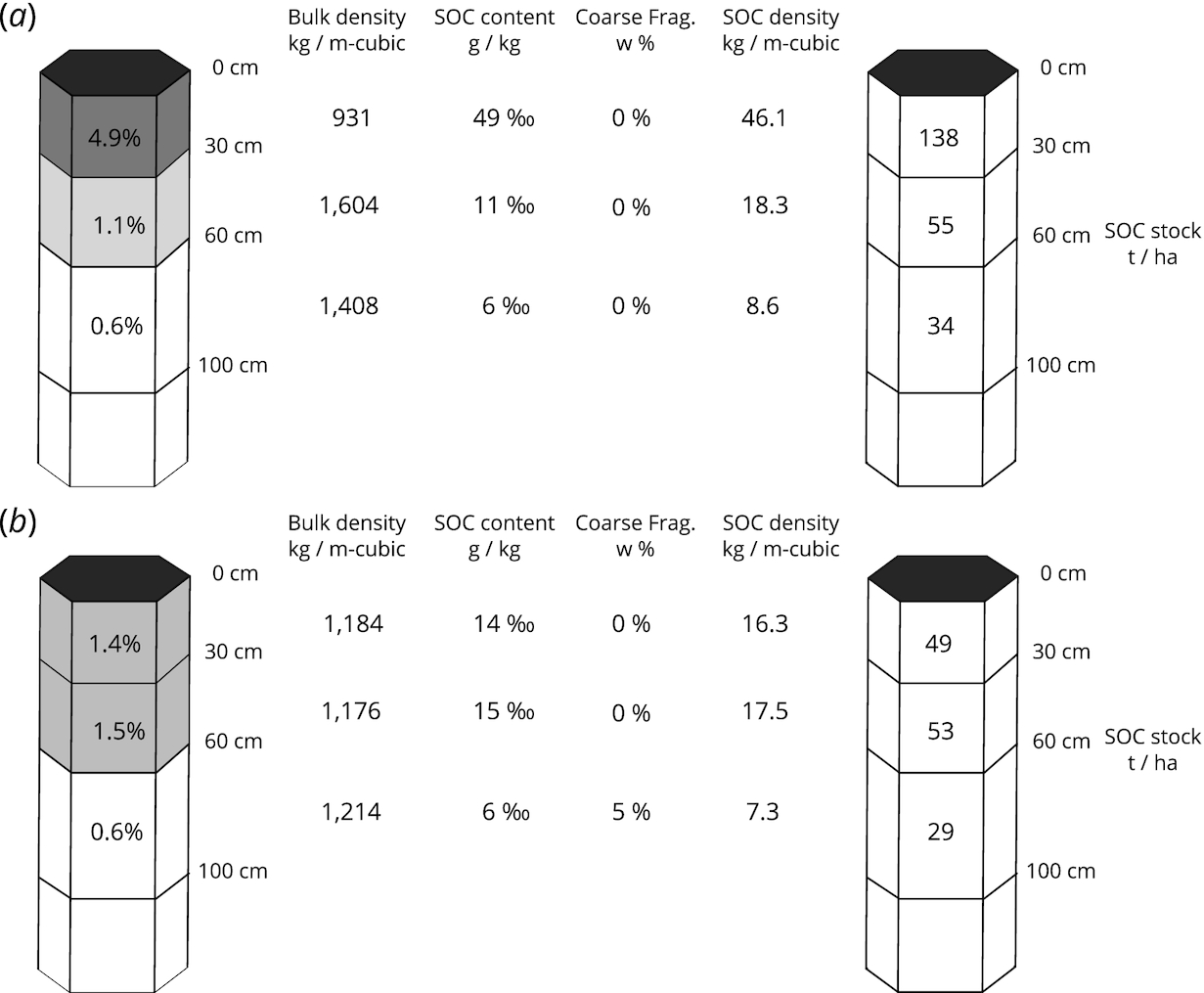
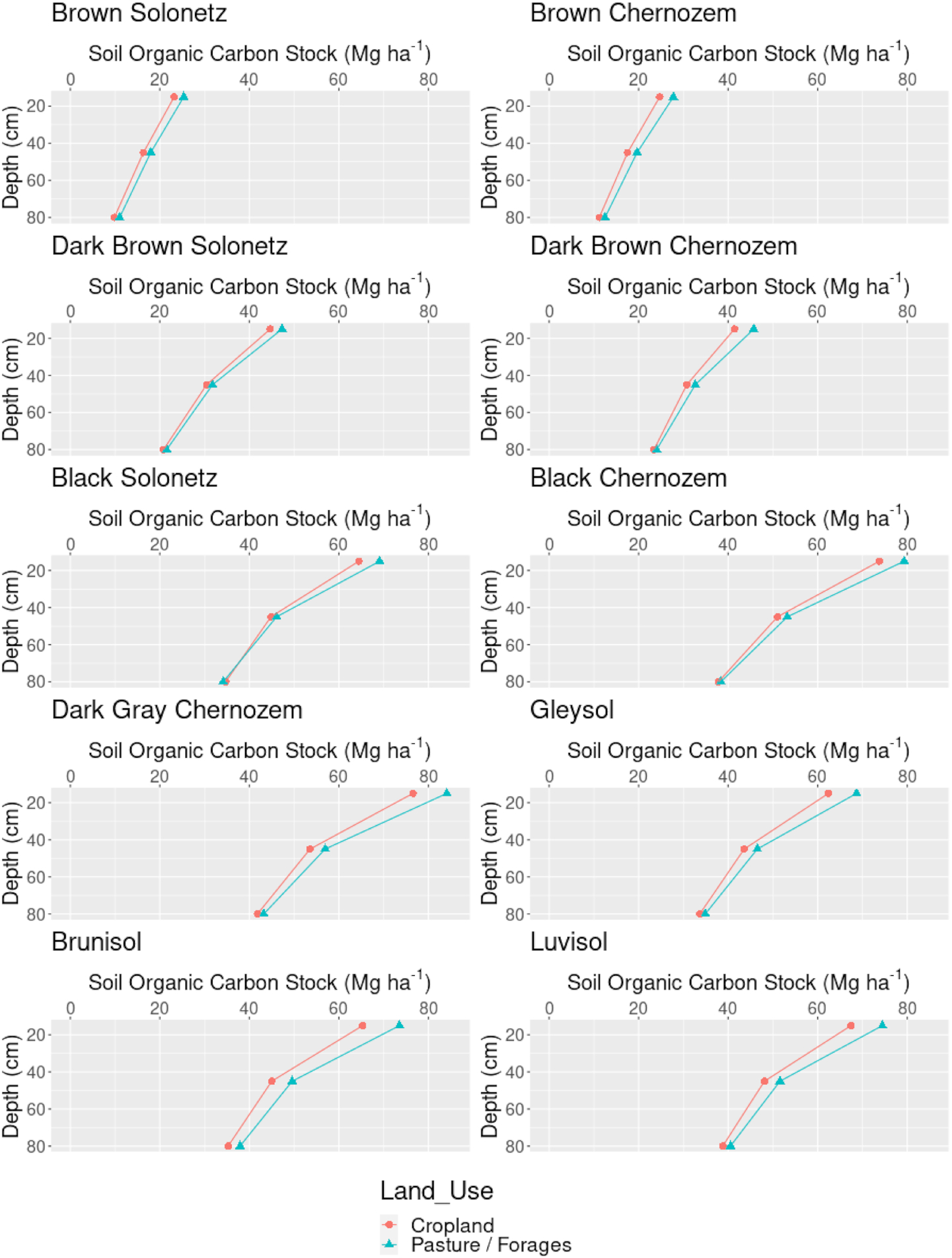
In this paper, we used a 3D multivariate approach as it enables relationships among soil properties and soil depth to be explicitly captured in the model. We derived SOC stocks from independently modeled and predicted SOC content (g/kg), bulk density of the fine earth fraction (kg/m3), and coarse fragments (dg/kg). After we produced maps for 3 soil variables at 5 depths (0, 15, 30, 60, and 100 cm), we aggregated values to standard depth intervals 0–30 cm and 30–100 cm and then derived SOC stocks for every pixel, including the uncertainty expressed as prediction error maps.
The SOC stocks in t/ha were derived using Nelson and Sommers (1983):where OCS was soil organic carbon stock, ORC was soil organic carbon mass fraction in permilles, HOT was horizon thickness in m, BLD was soil bulk density in kg/m3, and CRF was volumetric fraction of coarse fragments (>2 mm) in percent (Fig. 4).
(2)
Fig. 4.
The uncertainty of estimating SOC stocks in t/ha for a 3D multivariate approach can be derived using composite prediction errors (Hengl et al. 2014):where , , and are standard deviations of the predicted soil organic carbon content, bulk density, and coarse fragments (i.e. prediction errors), respectively.
(3)
2.5. Model validation
To validate accuracy of predicting SOC and bulk density, we used pseudo-probability samples (20% of total samples) and repeated model refitting as explained in Hengl et al. (2022b). This pseudo-probability resampling involved randomly subsampling the dataset while ensuring that all points used for validation were a minimum distance apart to get a better estimate of realistic map accuracy. Pseudo-probability resampling ensured that (a) spatial clustering was minimized and (b) spatial density of validation samples was constant. In practice this also means that whole soil sites are taken from training data and used for validation and that less clustered (relatively isolated) samples have a somewhat higher chance of being selected repeatedly.
We repeated the cross-validation process 5 times, with 30 km block sizes where all points within a block were withheld for use as validation data, and then derived average metrics per property. This procedure was only used for cross-validation, i.e., to determine the most realistic estimate of model performance: R square, RMSE, and Lin’s Concordance Correlation Coefficient (CCC) (Steichen and Cox 2002).
2.6. SOC aggregation per land use and soil type
Following development of the predictive soil maps for SOC stocks to a depth of 1 m, the resulting data were used to assess the influence of land use and soil type on SOC stocks in Alberta’s agricultural region. To assess SOC stocks by soil type, soil type polygons from the Agricultural Regions of Alberta Soil Inventory Database were used (Brierley et al. 2001). Land use was determined based on the Agriculture and Agri-food Canada Annual Space-Based Crop Inventory for Canada (Government of Alberta 2022).
Soil types were assessed at the order level following the Canadian System of Soil Classification (CSSC), except for Chernozemic soils that were assessed at the great group level to account for the large climatic gradient that influences SOC stocks for Chernozems in Alberta. Solonetzic soils were also separated by the Brown, Dark Brown, and Black subgroups to account for this same climate gradient. The categories were as follows, according to the CSSC (Soil Classification Working Group 1998) (with the World Reference Base classifications in brackets (IUSS Working Group WRB 2014)): Brown Solonetz (Solonetz), Brown Chernozem (Kastanozem aridic), Black Solonetz (Solonetz), Black Chernozem (Chernozem), Brunisol (Cambisol), Dark Brown Solonetz (Solonetz), Dark Brown Chernozem (Kastanozem Haplic), Dark Gray Chernozem (Greyzem), Gleysol (Gleysol), and Gray Luvisol (Albic Luvisol). An important feature to note is that Gleysols are known to have high carbon stores (Euliss et al. 2006), but they are distributed across all soil zones, so the values for this soil order were averaged across the climate gradient. Additionally, Gleysols are not extensively mapped as dominant soils in Alberta and many soil polygons contain Gleysols as minor soils.
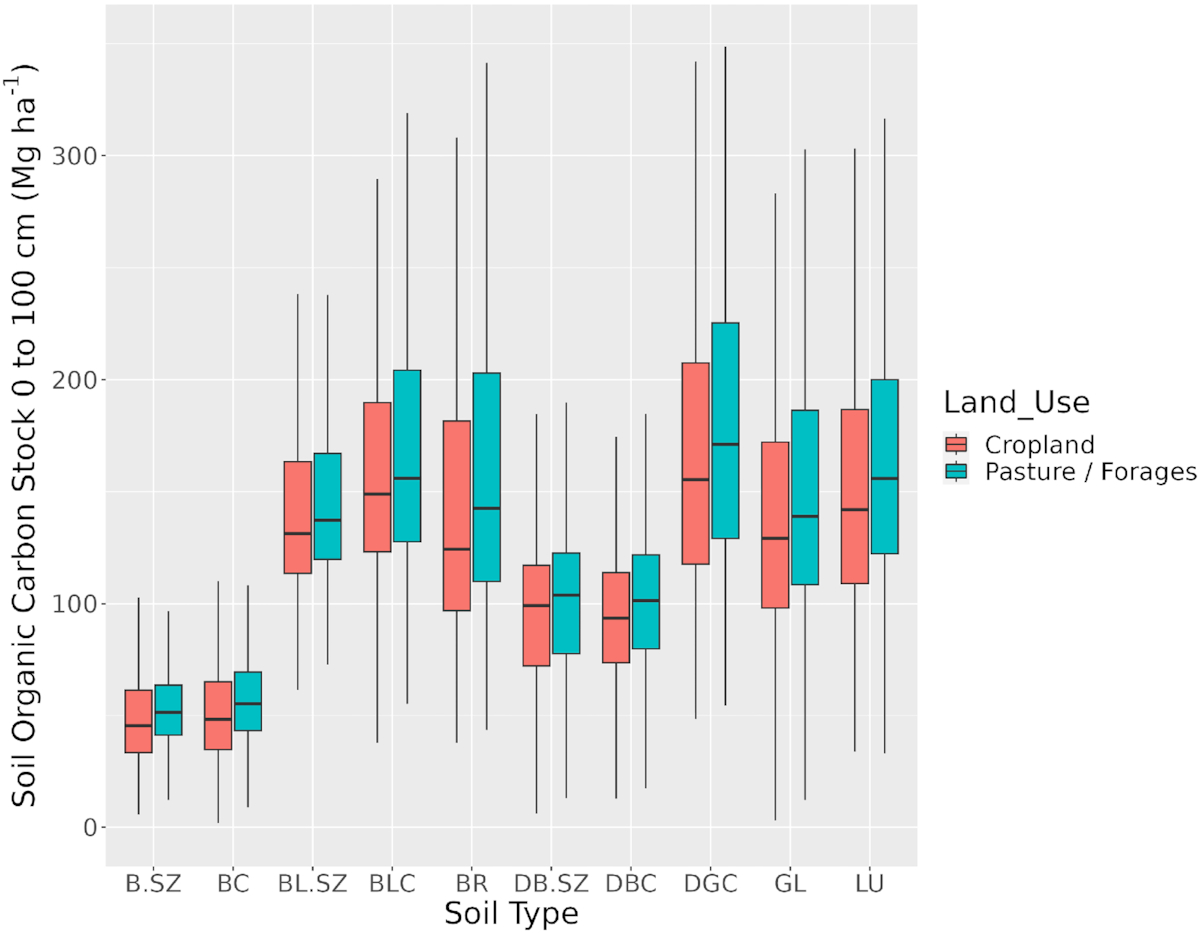
Total SOC stocks from 0 to 100 cm were calculated for land use categories of forested, cropland, grassland, shrubland, and wetland (Table 1). The forested land use category included conifer and broadleaf classes, cropland included all annual crop types, and grasslands included grassland, pastures, and forage land. SOC stocks from 0 to 100 cm, as a function of cropland and grassland land use categories, along with soil types, were then compared using a generalized least squares model with the nlme package in R (Pinheiro 2021). The interaction between soil type and land use type was tested, and it was significant (p < 0.01). Assessment of other land use classes was not examined with the generalized least squares model to simplify the results and because the vast majority of the training data came from cropland and grassland land use types.
Table 1.
| Land use type | Soil organic carbon stocks (Mg ha−1) |
|---|---|
| Forested | 120.5 |
| Cropland | 83.3 |
| Grassland, pastures, and forageland | 90.3 |
| Shrubland | 106.2 |
| Wetland | 103.5 |
Note: Annual crop land use types have been aggregated into a single cropland category.
3. Results
3.1. Variable importance and accuracy assessment
The results of model building using mlr showed contributions by different learners and variable importance based on the Random Forest feature selection. For modeling SOC content, all three algorithms were significant for predicting, and the stacking was thus highly efficient. The spatial cross-validation results for the final model had an R2 of 0.61 and CCC of 0.754 for SOC (see Fig. 5): Overall, Random Forest (Wright and Ziegler 2017) was the best learner, followed by Xgboost Chen et al. (2020) and Lasso and Elastic-Net Regularized Generalized Linear Models (regr.cvglmnet) (Friedman et al. 2020).
Fig. 5.
While all three learners were significant, it is important to note that the p value reached by the Random Forest component learner during the stacking was three orders of magnitude lower than the Xgboost component learner and six orders of magnitude lower than the Lasso and Elastic-Net component learner. A similar behavior was observed for the bulk density ensemble model: spatial cross-validation results reported an R2 of 0.68, RMSE of 0.21 g cm3, and CCC of 0.808, with Random Forest still performing as the best component learner, Xgboost as the second most important, and Lasso and Elastic-Net as the least important.
Even in this case, all three learners were significant but contrary to the SOC ensemble model. During the stacking for the bulk density model, the p value reached by the Random Forest component was only 1 order of magnitude lower than the Xgboost component learner and 16 times lower than the Lasso and Elastic-Net component. The variable importance analysis extracted from the Random Forest component showed that the top 10 most important covariates for mapping SOC and bulk density were similar (see Fig. 6): In both cases, soil depth was the most important covariate, with elevation the second most important for bulk density and the third most important for the SOC content.
Fig. 6.
The precipitation-related climate normals had the highest variable importance, with the cumulative precipitation of spring and fall being the most important ones for SOC content, while the precipitation for the month of June and the cumulative precipitation of fall being the most important for bulk density. The night temperatures recorded by MODIS LST were also included among the top 10 covariates but in quite different positions, together with mean summer precipitation. Consequently, when displaying predictions for the whole province, patterns of high to low SOC content primarily follow climate gradients (Fig. 7).
Fig. 7.
The SOC model however considered the Summer Heat Moisture index and the degree days below 18 °C (DD_18) as relevant, while the bulk density model didn’t consider those variables as important; on the other hand, the bulk density model considered the surface geological class Organic Deposits and the extreme minimum temperature over the last 30 years as important. Those variables were not identified as such for mapping SOC content. Overall, the results showed that SOC content, bulk density, and coarse fragments can be successfully mapped.
3.2. Comparison of predictions with previous maps
In the resulting predictive soil maps, SOC concentrations ranged (1st to 99th percentiles) from 0.4% to 6.1% for 0 to 30 cm, 0.2% to 2.8% for 30 to 60 cm, and 0% to 1.6% from 60 to 100 cm. SOC stocks ranged (1st to 99th percentiles) from 12 to 167 Mg ha−1 for 0 to 30 cm, 8 to 112 Mg ha−1 for 30 to 60 cm, 0 to 92 Mg ha−1 for 60 to 100 cm, and 20 to 364 Mg ha−1 for 0 to 100 cm. In both cases, a climatic trend of increasing SOC northward and westward was observed, driven by greater net precipitation.
Our laboratory results and results of modeling indicated that the predictions by Sothe et al. (2022) over-estimated the SOC content by 2× the actual values in some cases for Alberta agricultural soils (Fig. 8). The predictions in Sothe et al. (2022) over-estimated SOC concentrations by an average of 15.9 g kg−1 (Fig. 9). Locations in this study had an average SOC content of 27.5 g kg−1 compared to an average of 43.4 g kg−1 in Sothe et al. (2022), which is an overestimate of about 1.5–2 times. By comparison, the SoilGrids 250 m data (Hengl et al. 2017) underestimated SOC content by an average amount of 7.4 g kg−1, particularly for samples with higher SOC contents (Fig. 9). For comparison purposes, the soil depths for the SoilGrids data was splined in 1 cm intervals from 0 to 30 cm, and the average value for 0 to 30 cm was then calculated.
Fig. 8.
Fig. 9.
3.3. Soil organic carbon stocks per land use
In terms of overall SOC stocks, grasslands had significantly higher SOC stocks (0 to 100 cm), with an average of 90.3 Mg ha−1, compared to croplands with 83.3 Mg ha−1 (Table 1). Forests, shrublands, and wetlands all had significantly higher SOC stocks compared to grasslands and croplands. However, these land uses represent a smaller proportion of land uses compared to grasslands and croplands in Alberta’s agricultural region. Previous efforts estimated Alberta’s total agricultural SOC stocks to 1 m at 0.824 Pg (Bhatti et al. 2002). Significant carbon stocks are present in the boreal forest region of Alberta (Bhatti et al. 2002); however, the majority of this region is outside the scope of the study. The value for wetlands also needs to be interpreted with caution since the 30 m pixel size for the land use maps (Agriculture and Agri-Food Canada 2020) means that wetlands less than 900 m2 were accounted for in the grassland or cropland categories and not in the wetland category. Previous work has documented SOC stocks in wetlands to be approximately twice as much as no-till cropland (Euliss et al. 2006).
In summary, there was significant variability of SOC stocks within land use and soil type categories (Fig. 10), with Dark Gray Chernozems having the highest SOC stocks, followed by Black Chernozems. Brown Solonetz and Brown Chernozems had the lowest SOC stocks (Fig. 10). Overall, the majority of soil types had higher SOC stocks for grassland soils compared to cropland soils, with the exception of Brown Chernozems and Dark Brown Solonetzic soils (Table 2). Where an effect was present, the average increase was 2.1 Mg ha−1, with values ranging from 2.17 Mg ha−1 for Dark Brown Chernozems to 6.09 Mg ha−1 for Brunisolic soils (Table 2). Generally, greater increases in SOC stocks from grasslands occurred where net precipitation was higher (Hogg 1997). The standard land management unit in Alberta is a quarter section, which is equal to 64.75 ha. For a quarter section, grassland soils had 139–394 Mg of SOC more than cropland soils, depending on soil type, based on our model.
Fig. 10.
Table 2.
| Parameter | Model coefficient | Standard error | t value | p value |
|---|---|---|---|---|
| (Intercept) | 23.21 | 0.25 | 93.47 | 0 |
| Brown Chernozem (Kastanozem aridic) | 1.50 | 0.28 | 5.37 | 0 |
| Dark Brown Solonetz (Solonetz) | 21.45 | 0.36 | 59.42 | 0 |
| Dark Brown Chernozem (Kastanozem Haplic) | 18.21 | 0.27 | 66.63 | 0 |
| Black Solonetz (Solonetz) | 41.25 | 0.35 | 116.59 | 0 |
| Black Chernozem (Chernozem) | 50.57 | 0.27 | 188.71 | 0 |
| Dark Gray Chernozem (Greyzem) | 53.33 | 0.35 | 154.34 | 0 |
| Gray Luvisol (Albic Luvisol) | 44.24 | 0.27 | 161.11 | 0 |
| Brunisol (Cambisol) | 42.10 | 0.55 | 76.00 | 0 |
| Gleysol (Gleysol) | 39.19 | 0.28 | 141.69 | 0 |
| Grassland | 2.13 | 0.415 | 5.14 | 0 |
| Brown Chernozem: Grassland | 0.93 | 0.48 | 1.94 | 0.05 |
| Dark Brown Solonetz: Grassland | 0.51 | 0.62 | 0.82 | 0.41 |
| Dark Brown Chernozem: Grassland | 2.17 | 0.47 | 4.64 | 0 |
| Black Solonetz: Grassland | 2.51 | 0.62 | 4.08 | 0 |
| Black Chernozem: Grassland | 3.41 | 0.45 | 7.52 | 0 |
| Dark Gray Chernozem: Grassland | 5.43 | 0.59 | 9.25 | 0 |
| Gray Luvisol: Grassland | 4.88 | 0.46 | 10.59 | 0 |
| Brunisol: Grassland | 6.09 | 0.85 | 7.19 | 0 |
| Gleysol: Grassland | 4.15 | 0.47 | 8.88 | 0 |
Note: A significant interaction (p < 0.01) was present among soil type and land use. Soil types are listed according to the Canadian System of Soil Classification with the closest corresponding World Reference Base classification in brackets. The intercept contains the cropland and the Brown Solonetz (Solonetz) factors.
The Dark Brown Solonetzic soils had higher SOC stocks than Dark Brown Chernozems, which was unexpected. This could be due to the Dark Brown Solonetzic soils having a higher proportion of land as grassland compared to Dark Brown Chernozems. While there was no grassland effect for Dark Brown Solonetzic soils, grasslands were associated with higher SOC in the Dark Brown Chernozems. It is notable that the SOC stocks below 30 cm made up a relatively higher proportion of the total SOC stocks (Fig. 11). The increased SOC stocks associated with grassland soils were also generally observed at the 0–30 and 30–60 cm depths (Fig. 11).
Fig. 11.
Overall, the fraction of SOC stocks in the upper 30 cm ranged from 43% to 47%, with an average of 46% across soil types (Fig. 11). These results are comparable to grassland soil carbon stocks in Great Britain that were estimated to contain more than 60% of their carbon below 30 cm (Ward et al. 2016). The stocks of SOC in a re-established grassland in the Canadian Prairie province of Manitoba by comparison had 40% of its carbon in the top 30 cm, compared to SOC stocks to 120 cm (Bell et al. 2012). Overall, this work further supports the inclusion of deeper soil horizons as part of SOC stock assessments, particularly in grasslands, and subsoil horizons need to be considered as part of global SOC cycles (Rumpel and Kögel-Knabner 2011).
4. Discussion
4.1. Accuracy levels and key explanatory variables
One of the advantages of this study is that a majority of training points used to determine SOC stocks were based on a systematic survey by a single team with robust mechanical instruments. In addition, we used an excessive list of covariate layers at high spatial resolution, closely matching sampling locations determined with high spatial accuracy (location RMSE < 10 m). Consequently, the results of accuracy assessment using multi-fold cross-validation with careful subsampling of training points showed that the models were significant with CCC at 0.754 and 0.888 for log-SOC and bulk density, respectively (Fig. 5), with no significant over- or underestimation of values. This gave us confidence to use these models to produce predictions for Alberta’s agricultural land at a spatial resolution of 30 m (maps available at https://g3w.soils.app/en/map/alberta-soil-carbon/).
The results of laboratory analyses and modeling (surprisingly) showed that >15% of total SOC stocks were located in sub-soil (deeper than >30 cm), which was deeper than expected. Soil scientists usually expect that SOC content drops exponentially with soil depth (following a log-log model), but it appears that, because Alberta has significant areas under grasslands/pastureland, a large stock of SOC is located at >30 cm and should not be ignored.
4.2. Large discrepancies in the baseline SOC stock between previous and this study
Predictive soil mapping efforts focused on the Canadian prairies have so far been limited. Recent Canada-wide work at a spatial scale of 250 m has included the Canadian Prairies; however, much of the training data were more heavily weighted to Canada’s forested regions (Sothe et al. 2021, 2022). Mapping of historical topsoil SOC has been completed in the neighboring province of Saskatchewan at resolutions finer than 250 m (Sorenson et al. 2021), but SOC stocks have not been previously mapped at resolutions finer than 250 m in Alberta.
Our predictions indicated that the results from Sothe et al. (2022) most likely over-estimate SOC stocks for Alberta (Fig. 9) and possibly large parts of Canada. We can only speculate as to why the predictions produced by Sothe et al. (2022) were biased high compared to the laboratory data in this study. A likely explanation is that training points used by Sothe et al. (2022) over-represented forest areas and wetlands, which are typically richer in SOC. Our results consistently showed that for most farms in this study, Alberta SOC stocks range from 30 to 120 Mg ha−1 (0–30 cm). Another possible explanation is that the loss on ignition data in the Sothe et al. (2022) training data may over-estimate carbon concentrations (Jensen et al. 2018). Using the Sothe et al. (2022) results underestimates the potential for Alberta soils to sequester carbon. This highlights the need for an updated soil carbon database in Canada, collected across Canada’s major physiographic regions using current laboratory methods to generate accurate and up-to-date SOC maps.
4.3. SOC stocks per main land cover
The higher SOC stocks in grassland soils are corroborated by other studies that have documented increased SOC stocks when land is converted to perennial crops. Converting crop to pasture was associated with an increase of 19% in SOC stocks in Australia and the USA (Guo and Gifford 2002). However, grassland versus cropland SOC stock comparisons have been limited in the Canadian Prairies. Changes in SOC stocks of 3–14 Mg ha−1 were observed after converting from arable cropland to perennial crops in Alberta over a 13–25-year time period (VandenBygaart et al. 2010). Re-establishment of perennial vegetation led to SOC stock gains of 6.8 Mg ha−1 in east central Saskatchewan (Mensah et al. 2003). Both of these studies focused on specific research sites rather than monitoring changes over extensive areas. An important factor to note is that confounding factors, such as soil texture, were not assessed in this study. Grasslands in Alberta would on average be expected to have coarser textured soils, as finer textured soils were preferentially cultivated for arable crops historically in the Canadian Prairies.
In general, the results of our study showed lower SOC contents compared to Sothe et al. (2022). For the prairies, their study had average SOC contents of 57.2 g kg−1 at 0 cm, 49.3 g kg−1 at 5 cm, 28.2 g kg−1 at 15 cm, 17.78 g kg−1 at 30 cm, and 11.7 g kg−1 at 60–100 cm. In contrast, data from our study (excluding one site with organic soils) had average SOC values of 36.5 g kg−1 from 0 to 15 cm, 18.8 g kg−1 from 15 to 30 cm, 11.1 g kg−1 from 30 to 60 cm, and 6.0 g kg−1 from 60 to 100 cm.
5. Conclusion
This study represents the most up-to-date and finest spatial resolution SOC stock maps for the Canadian Province of Alberta. The results of this study indicated Alberta’s grasslands have greater stores of SOC stocks than croplands, and this work highlights the importance of grassland soils as a store of carbon. Across most soil types in Alberta, grasslands showed consistent increases in SOC stocks compared to croplands, particularly in soil types associated with higher net precipitation. Previous national estimates by Sothe et al. (2021) significantly over-estimate SOC stocks for agricultural land in Alberta, which might be due to the spatial resolution and/or bias in the training points used representing mainly forest soils. Overall, the lower SOC contents in this study compared to recent Canada-wide mapping indicate that improved and updated soil databases are essential for accurate SOC stock estimates in Canada. The next steps for this work is to obtain enough finer resolution imagery to test mapping at scales finer than 30 m and to test algorithms for mapping SOC in a space–time domain as a dynamic phenomena.
Acknowledgements
This work was funded by the Government of Canada and the Government of Alberta through the Canadian Agricultural Partnership.
References
Agriculture and Agri-Food Canada. 2020. Annual space-based crop inventory for Canada, 2009–2020.
Alberta Geological Survey 2020. 2020. Bedrock topography of Alberta, version 2 (gridded data, ASCII format). Alberta Energy Regulator/Alberta Geological Survey, Edmonton, AB.
Bai Y., Cotrufo M.F. 2022. Grassland soil carbon sequestration: current understanding, challenges, and solutions. Science, 377(6606): 603–608.
Behrens T., Schmidt K., MacMillan R.A., Rossel R.V. 2018. Multiscale contextual spatial modelling with the Gaussian scale space. Geoderma, 310: 128–137.
Bell L., Sparling B., Tenuta M., Entz M. 2012. Soil profile carbon and nutrient stocks under long-term conventional and organic crop and alfalfa-crop rotations and re-established grassland. Agriculture, Ecosystems & Environment, 158: 156–163.
Bhatti J.S., Apps M.J., Tarnocai C. 2002. Estimates of soil organic carbon stocks in central Canada using three different approaches. Canadian Journal of Forest Research, 32(5): 805–812.
Bischl B., Lang M., Kotthoff L., Schiffner J., Richter J., Studerus E., et al. 2016. mlr: machine learning in R. The Journal of Machine Learning Research, 17(1): 5938–5942.
Brierley J., Martin T., Spiess D. 2001. AGRASID: agricultural regions of Alberta soil inventory database. Agriculture and Agri-Food Canada, Alberta Agriculture. Food and Rural Development, Edmonton, AB.
Brus D. 2021. Spatial sampling with R. CRC The R Series. Taylor & Francis, London.
Cathcart J., Mason H., Sey B., Heinz J., Cannon K. 2008. Assessment of environmental sustainability in Alberta’s Agricultural Watersheds Project. Alberta Agriculture and Rural Development, Edmonton, AB.
Chen T., Guestrin C. 2016. Xgboost. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.
Chen T., He T., Benesty M., Khotilovich V., Tang Y. 2020. Xgboost: extreme gradient boosting. R package version 0.4-2. pp. 1–4.
Conant R.T., Cerri C.E., Osborne B.B., Paustian K. 2017. Grassland management impacts on soil carbon stocks: a new synthesis. Ecological Applications, 27(2):662–668.
Ellili Y., Walter C., Michot D., Pichelin P., Lemercier B. 2019. Mapping soil organic carbon stock change by soil monitoring and digital soil mapping at the landscape scale. Geoderma, 351: 1–8.
Euliss N.H., Jr., Gleason R.A., Olness A., McDougal R., Murkin H., Robarts R., et al. 2006. North American prairie wetlands are important nonforested land-based carbon storage sites. Science of the Total Environment, 361(1–3): 179–188.
Fisette T., Davidson A., Daneshfar B., Rollin P., Aly Z., Campbell L. 2014. Annual space-based crop inventory for Canada: 2009–2014. In 2014 IEEE Geoscience and Remote Sensing Symposium. IEEE. pp. 5095–5098.
Friedman J., Hastie T., Tibshirani R., Narasimhan B., Tay K., Simon N., Qian J. 2020. glmnet: lasso and elastic-net regularized generalized linear models. R package version 4.0-2.
Gasch C.K., Hengl T., Gräler B., Meyer H., Magney T.S., Brown D.J. 2015. Spatio-temporal interpolation of soil water, temperature, and electrical conductivity in 3D+ T: The Cook Agronomy Farm data set. Spatial Statistics, 14: 70–90.
Government of Alberta. 2022. Agricultural regions of Alberta soil inventory database (AGRASID). Food and Rural Development, Edmonton, AB.
Guevara M., Arroyo C., Brunsell N., Cruz C.O., Domke G., Equihua J., et al. 2020. Soil organic carbon across Mexico and the conterminous united states (1991–2010). Global Biogeochemical Cycles, 34(3).
Guo L.B., Gifford R.M. 2002. Soil carbon stocks and land use change: a meta analysis. Global Change Biology, 8(4): 345–360.
Hengl T., MacMillan R. 2019. Predictive soil mapping with R. OpenGeoHub Foundation, Wageningen.
Hengl T., de Jesus J.M., MacMillan R.A., Batjes N.H., Heuvelink G.B., Ribeiro E., et al. 2014. Soilgrids1km—global soil information based on automated mapping. PloS ONE, 9(8): e105992.
Hengl T., de Jesus J.M., Heuvelink G.B., Gonzalez M.R., Kilibarda M., Blagotić A., et al. 2017. Soilgrids250m: global gridded soil information based on machine learning. PloS ONE, 12(2): e0169748.
Hengl T., Miller M.A., Križan J., Shepherd K.D., Sila A., Kilibarda M., et al. 2021. African soil properties and nutrients mapped at 30 m spatial resolution using two-scale ensemble machine learning. Scientific Reports, 11(1): 1–18.
Hengl T., Parente L., Bonannella C. 2022a. Spatial and spatiotemporal interpolation/prediction using ensemble machine learning. OpenGeoHub foundation, Wageningen, the Netherlands.
Hengl T., Parente L., Wheeler I. 2022b. Spatial sampling and resampling for machine learning. OpenGeoHub foundation, Wageningen, the Netherlands.
Hogg E.H. 1997. Temporal scaling of moisture and the forest-grassland boundary in western canada. Agricultural and Forest Meteorology, 84(1–2):115–122.
IUSS Working Group WRB. 2014. World reference base for soil resources 2014. International soil classification system for naming soils and creating legends for soil maps. In World Soil Resources Reports No. 106, IUSS. pp. 1–191.
Jaxa. 2015. Alos global digital surface model “alos world 3d–30m” (aw3d30).
Jensen J., Christensen B., Schjønning P., Watts C., Munkholm L. 2018. Converting loss-on-ignition to organic carbon content in arable topsoil: pitfalls and proposed procedure. European Journal of Soil Science, 69(4): 604–612.
Jobbagy E.G., Jackson R.B. 2000. The vertical distribution of soil organic carbon and its relation to climate and vegetation. Ecological Applications, 10(2): 423–436.
KC K.B., Green A.G., Wassmansdorf D., Gandhi V., Nadeem K., Fraser E.D. 2021. Opportunities and trade-offs for expanding agriculture in Canada’s north: an ecosystem service perspective. FACETS, 6: 1728–1752.
Lal R. 2022. Soil organic carbon and feeding the future: basic soil processes. Advances in soil science. CRC Press.
Lal R., Smith P., Jungkunst H.F., Mitsch W.J., Lehmann J., Nair P.R., et al. 2018. The carbon sequestration potential of terrestrial ecosystems. Journal of Soil and Water Conservation, 73(6): 145A–152A.
Lu B., Hardin J. 2021. A unified framework for random forest prediction error estimation. Journal of Machine Learning Research, 22(8): 1–41.
Ma Y., Minasny B., McBratney A., Poggio L., Fajardo M. 2021. Predicting soil properties in 3d: should depth be a covariate? Geoderma, 383: 114794.
Mahony C.R., Wang T., Hamann A., Cannon A.J. 2022. A global climate model ensemble for downscaled monthly climate normals over North America. International Journal of Climatology, 42: 5871–5891.
Mensah F., Schoenau J., Malhi S. 2003. Soil carbon changes in cultivated and excavated land converted to grasses in east-central saskatchewan. Biogeochemistry, 63(1): 85–92.
Minasny B., McBratney A.B. 2006. A conditioned latin hypercube method for sampling in the presence of ancillary information. Computers & Geosciences, 32(9): 1378–1388.
Nelson D., Sommers L. 1983. Total carbon, organic carbon, and organic matter. In Methods of soil analysis. Part 2 chemical and microbiological properties. Vol. 9. Wiley Online Library. pp. 539–579.
Pinheiro J. 2021. nlme: linear and nonlinear mixed effects models. R package version 3.1-96. R package version 3.1-159.
Poggio L., De Sousa L.M., Batjes N.H., Heuvelink G., Kempen B., Ribeiro E., Rossiter D. 2021. SoilGrids 2.0: producing soil information for the globe with quantified spatial uncertainty. Soil, 7(1): 217–240.
Potapov P., Hansen M.C., Kommareddy I., Kommareddy A., Turubanova S., Pickens A., et al. 2020. Landsat analysis ready data for global land cover and land cover change mapping. Remote Sensing, 12(3): 426.
Ramankutty N., Evan A.T., Monfreda C., Foley J.A. 2008. Farming the planet: 1. geographic distribution of global agricultural lands in the year 2000. Global Biogeochemical Cycles, 22(1).
Roper W.R., Robarge W.P., Osmond D.L., Heitman J.L. 2019. Comparing four methods of measuring soil organic matter in North Carolina soils. Soil Science Society of America Journal, 83(2): 466–474.
Roudier P. 2021. CRAN. R package version 0.9.0.
Roudier P., Beaudette D., Hewitt A. 2012. A conditioned Latin hypercube sampling algorithm incorporating operational constraints. CRC Press, London. pp. 227–231.
Rumpel C., Kögel-Knabner I. 2011. Deep soil organic matter—a key but poorly understood component of terrestrial C cycle. Plant and Soil, 338(1): 143–158.
Sanderman J., Hengl T., Fiske G., Solvik K., Adame M.F., Benson L., et al. 2018. A global map of mangrove forest soil carbon at 30 m spatial resolution. Environmental Research Letters, 13(5): 055002.
Scharlemann J.P., Tanner E.V., Hiederer R., Kapos V. 2014. Global soil carbon: understanding and managing the largest terrestrial carbon pool. Carbon Management, 5(1): 81–91.
Schratz P., Muenchow J., Iturritxa E., Richter J., Brenning A. 2019. Hyperparameter tuning and performance assessment of statistical and machine-learning algorithms using spatial data. Ecological Modelling, 406: 109–120.
Soil Classification Working Group. 1998. The Canadian system of soil classification. 3rd ed. Agriculture and Agri-Food Canada Publication 1646. Agriculture and Agri-Food Canada. p. 187.
Sorenson P., Shirtliffe S., Bedard-Haughn A. 2021. Predictive soil mapping using historic bare soil composite imagery and legacy soil survey data. Geoderma, 401: 115316.
Sothe C., Gonsamo A., Arabian J., Kurz W.A., Finkelstein S.A., Snider J. 2021. Large soil carbon storage in terrestrial ecosystems of Canada. Global Biogeochemical Cycles, 36:e2021GB007213.
Sothe C., Gonsamo A., Arabian J., Snider J. 2022. Large scale mapping of soil organic carbon concentration with 3D machine learning and satellite observations. Geoderma, 405: 115402.
Steichen T.J., Cox N.J. 2002. A note on the concordance correlation coefficient. Stata J, 2(2): 183–189.
Tifafi M., Guenet B., Hatté C. 2018. Large differences in global and regional total soil carbon stock estimates based on SoilGrids, HWSD, and NCSCD: intercomparison and evaluation based on field data from USA, England, Wales, and France. Global Biogeochemical Cycles, 32(1): 42–56.
VandenBygaart A., Bremer E., McConkey B., Janzen H., Angers D., Carter M., et al. 2010. Soil organic carbon stocks on long-term agroecosystem experiments in Canada. Canadian Journal of Soil Science, 90(4): 543–550.
Wadoux A.M.C., Heuvelink G.B., De Bruin S., Brus D.J. 2021. Spatial cross-validation is not the right way to evaluate map accuracy. Ecological Modelling, 457: 109692.
Ward S.E., Smart S.M., Quirk H., Tallowin J.R., Mortimer S.R., Shiel R.S., et al. 2016. Legacy effects of grassland management on soil carbon to depth. Global Change Biology, 22(8): 2929–2938.
Witjes M., Parente L., van Diemen C.J., Hengl T., Landa M., Brodskỳ L., et al. 2022. A spatiotemporal ensemble machine learning framework for generating land use/land cover time-series maps for europe (2000–2019) based on LUCAS, CORINE and GLAD landsat. PeerJ, 10: e13573.
Wolters E., Dierckx W., Iordache M.D., Swinnen E. 2014. PROBA-V products user manual. VITO, Mol, Belgium.
Wright M.N., Ziegler A. 2017. ranger: a fast implementation of Random Forests for high dimensional data in C++ and R. Journal of Statistical Software, 77(1): 1–17.
Information & Authors
Information
Published In
FACETS
Volume 8 • January 2023
Pages: 1 - 17
Editor: Christoph E. Geiss
History
Received: 16 March 2023
Accepted: 16 June 2023
Version of record online: 7 September 2023
Notes
The article was originally published with minor errors (typographical in abstract) that have now been corrected.
Copyright
© 2023 Authors Hengl, Sorenson, Parente, Cornish, Battigelli, Bonannella, and Nichols, and The Crown. This work is licensed under a Creative Commons Attribution 4.0 International License (CC BY 4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Data Availability Statement
Data are available under certain conditions. Due to privacy concerns, the data are not publicly available. The data are available from the corresponding author with a data access agreement.
Key Words
Sections
Subjects
Authors
Author Contributions
Conceptualization: TH, KC, MG, KN
Data curation: KC, JB, MG, KN
Formal analysis: TH, PS, LP, CB
Funding acquisition: KC, KN
Investigation: KC
Methodology: TH, PS, LP, CB
Software: TH, PS
Writing – original draft: TH, PS
Writing – review & editing: TH, PS, KC, JB, MG
Competing Interests
Competing interests: The authors declare there are no competing interests.
Funding Information
Canadian Agricultural Partnership
Metrics & Citations
Metrics
Other Metrics
Citations
Cite As
Tomislav Hengl, Preston Sorenson, Leandro Parente, Kimberly Cornish, Jeffrey Battigelli, Carmelo Bonannella, Monika Gorzelak, and Kris Nichols. 2023. Assessment of soil organic carbon stocks in Alberta using 2-scale sampling and 3D predictive soil mapping. FACETS.
8(): 1-17. https://doi.org/10.1139/facets-2023-0040
Export Citations
If you have the appropriate software installed, you can download article citation data to the citation manager of your choice. Simply select your manager software from the list below and click Download.
There are no citations for this item