1. Introduction
In the marine environment, most cultured finfish are reared in open-water net pens, where abiotic and biotic exchanges occur between the farm and the environment (
Milewski and Smith 2019;
Carballeira Braña et al. 2021). Pathogens and parasites carried by wild hosts migrating in the vicinity of aquaculture sites present a risk to the farm, as these can be transferred from wild hosts to farmed species (i.e., spill over) and amplified within the site, resulting in significant losses and costs to the industry (
Grant and Jones 2011). These parasites and pathogens can then be spilled back into the environment, and in turn infect wild species, as well as farmed species located on adjacent sites (
Ford and Myers 2008;
Johnsen et al. 2021). Understanding the transport and dispersal of parasites and pathogens is thus important to assess the risk of disease transfer between wild and farmed conspecifics and guide implementation of efficient management practices that can reduce this risk or mitigate the impacts.
Progress in the development of biophysical models, which couple physical oceanographic models with epidemiological models of infectious agents, has allowed the emergence of new tools to characterize the transport and dispersal networks of pathogens and parasites in marine ecosystems (
Page et al. 2005;
Gustafson et al. 2007;
Chang et al. 2014;
Foreman et al. 2015a). Physical models can capture regional oceanographic conditions, such as currents, temperature, and salinity, and biophysical models link these parameters with pathogen or parasite dynamics to improve predictive abilities. For instance, models of outbreaks and spread of parasites like sea lice (
Lepeophtheirus salmonis) have been expanded to include biological information, such as host density, life cycle stages, and vertical migration behavior (
Johnsen et al. 2016;
Salama et al. 2018;
Cantrell et al. 2020a). As with parasites, the dispersion of pathogens, such as the infectious hematopoietic necrosis virus (IHNV), was also simulated by a hydrodynamic model wherein biological features were incorporated, including shedding rate, decay rate, and minimum infectious dose (
Foreman et al. 2015b).
Most dispersal models of waterborne pathogens typically simulate one average or one worst case scenario of infection as a simplifying assumption without integrating the epidemic progression of the disease (
Olivares et al. 2015;
Foreman et al. 2015b;
Cantrell et al. 2020b). Infection and viral shedding are dynamic processes, evolving over the course of an outbreak, with variable viral abundance released into the water, and dispersed in turn by ocean conditions. As infection worsens for individual fish, the population-level shedding rate will increase, up to a peak level from which it will decrease due to mortality, recovery, immunity, culling, etc. (
Gregory et al. 2009;
Mardones et al. 2009;
Qviller et al. 2020). Viral inactivation in the marine environment is another important factor that impacts virus infectivity and disease transmission (
Oidtmann et al. 2018). Ultraviolet (UV) radiation, native microbes in water, and temperature are some of the main factors leading to viral decay and eventual loss of infectivity with time (
Tapia et al. 2013;
Vike et al. 2014;
Pinon and Vialette 2018). Temporal variation in infective particle release, either caused by natural or human intervention, needs to be captured by incorporating the infection dynamics of the outbreak and the inactivation processes into models, which enables more realistic scenarios of simulated pathogen transmission, better predictions of outcome, and, ultimately, more efficient management actions to be undertaken.
Many studies of infectious disease models in terrestrial animals have developed methods to integrate dynamic infection processes (
Garner and Beckett 2005;
Jenness et al. 2018). A notable example is the Davis Animal Disease Simulation model (DADS) (
Bates et al. 2003), which was based on a susceptible-exposed-infectious-removed (SEIR) compartmental model (
Kermack and McKendrick 1927). A later-developed version, the DTU-DADS-ASF (Danish Technical University - Davis Animal Disease Model -African Swine Fever) model (
Halasa et al. 2019), was adapted to simulate infectious salmon anemia virus (ISAV) and IHNV infections within and between aquaculture sites in marine environments, with seaway distance as the primary determinant of waterborne pathogen transmission (
Romero et al. 2021,
2022). This model provides an efficient tool to capture the dynamic evolution of infected fish numbers within a farm, which determines virus shedding and release. However, the impacts of the hydrodynamic oceanic environment and decay processes on pathogen dispersal have not been included. As a result, the simulations of spatiotemporal dispersal are limited due to the unaccounted-for effects of hydrodynamics and biological components on the virus.
Listed as a notifiable disease by the World Organization for Animal Health (WOAH), ISAV has caused severe economic losses in the Atlantic salmon (
Salmo salar) aquaculture industry between the late 1990s and early 2000s, and it continues to create an economic burden (
Gagné and LeBlanc 2018). These losses and potential pressures to the environment have led to significant efforts in salmon aquaculture regulation and management (
Chang et al. 2014). Notably, the tidal excursion area and overlapping scales of water exchange for dispersing ISAV particles have been modelled with a 3-D tidal circulation and particle tracking model to support the establishment of bay management areas (BMAs) in southwestern New Brunswick (NB), Canada (
Page et al. 2005). In these studies, the simulation of viral dispersal focused primarily on the development and application of physical models with recommendations to incorporate pathogen dynamics in future developments (
Graham et al. 2007;
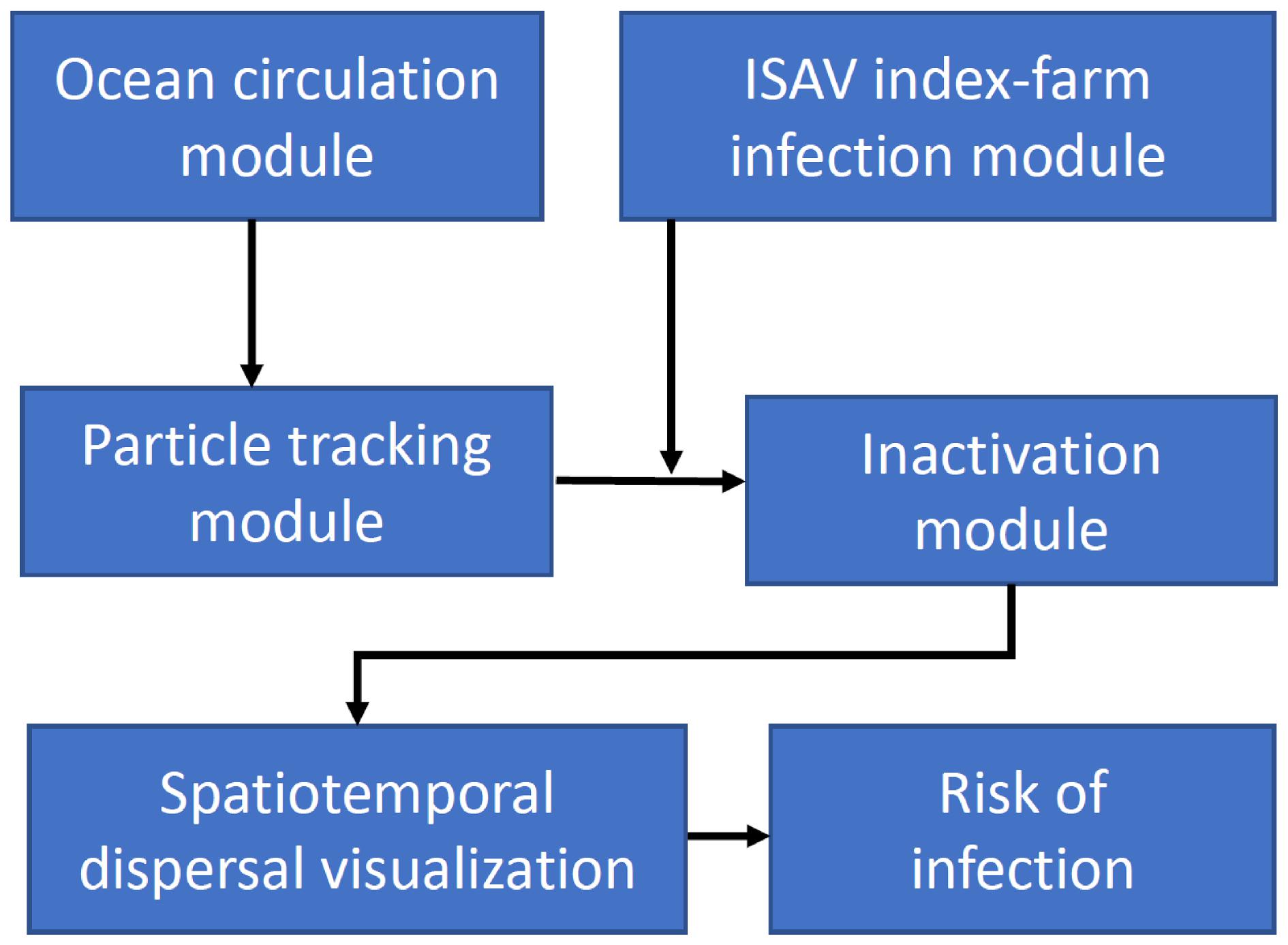
Johnsen et al. 2014). In this study, we developed a four-module framework that includes hydrodynamics, ISAV infection dynamics, viral inactivation, and risk of infection for surrounding environments to simulate the transport and dispersal of ISAV from Atlantic salmon farms in the Quoddy Region of New Brunswick, Canada, and Maine, USA. The integration of these modules aims to bridge the hydrodynamic model and biological components of ISAV, especially the dynamic progression of an infection within an outbreak, which is currently lacking in virus dispersal models. By coupling the dynamics of a viral infection with hydrodynamic processes rather than simply using a given infection scenario, more realistic scenarios of the spatiotemporal virus distribution during an entire outbreak are produced.
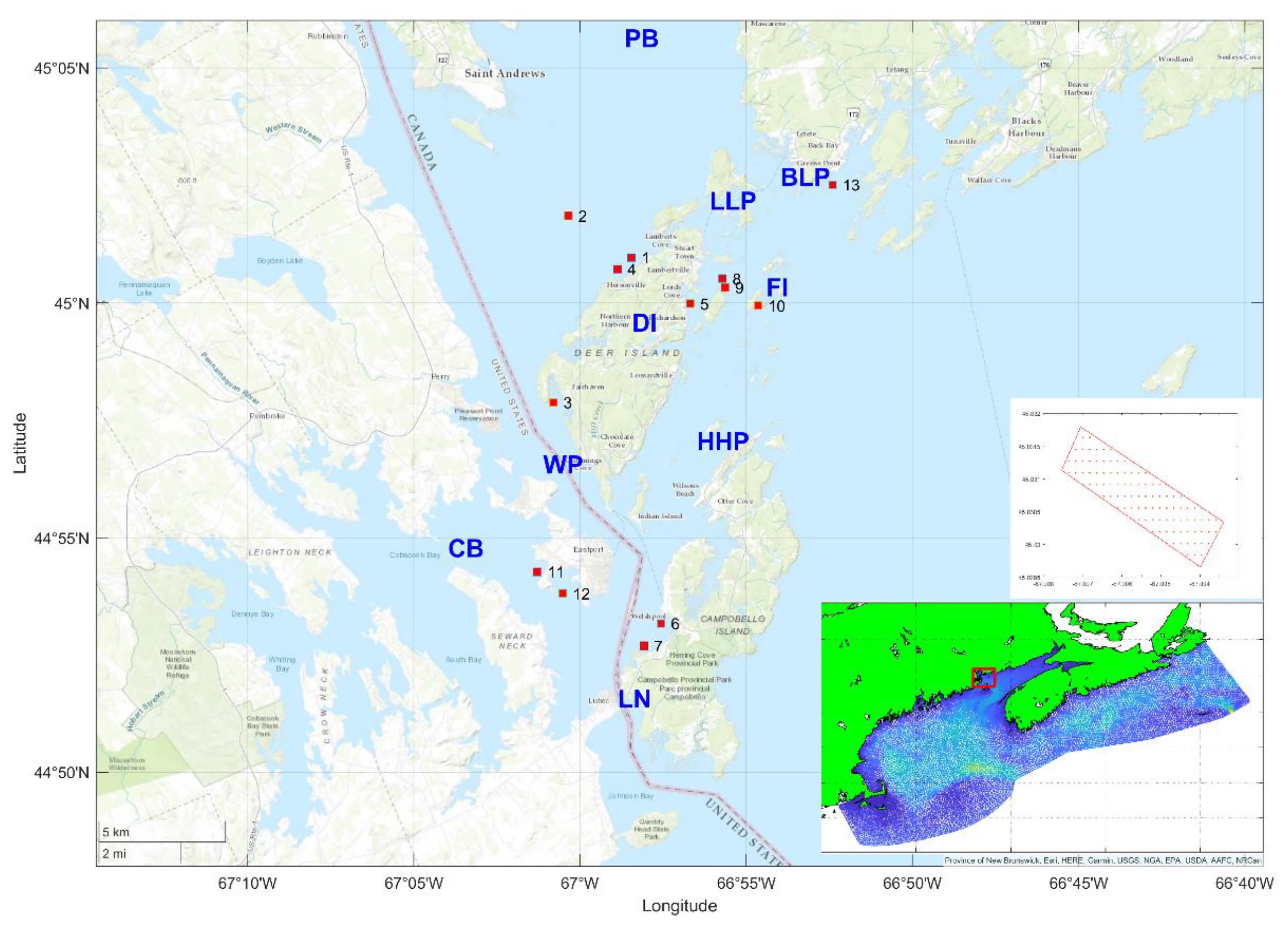
The Quoddy Region is an important salmon aquaculture area in the southwestern end of the Bay of Fundy and is bordered by the Canadian province of New Brunswick and the U.S. state of Maine (
Fig. 1). It is a unique region with extreme tidal ranges (i.e., 7–8 m), freshwater inputs, and wind-driven surface currents (
Trites and Garrett 1983;
Greenberg et al. 2005). The first successful salmon farming in Atlantic Canada began in this region in 1979 (
Anderson 2007;
Chang et al. 2014). There are currently more than 50 salmon farming lease sites in the Quoddy Region, though less than half of the sites are active at any given time. Although ISA disease outbreaks in New Brunswick are currently a less severe issue than in past decades as a result of improved disease control strategies, the virus is still regularly detected, contributing to economic and environmental pressure in the region (
Canadian Food Inspection Agency 2022). Hence, a better understanding of the dispersal of ISAV in the area is required for risk assessment of disease transmission and aquaculture management.
4. Discussion
In this study, we developed a numerical modelling framework to simulate the dispersal of ISAV following a hypothetical outbreak at selected salmon farms in the Quoddy Region by coupling physical ocean circulation and particle tracking models with biological models, including a dynamic infection module and a virus inactivation module. Using this framework, viral dispersal maps for farms were produced, which indicated that the concentration level of ISAV varied spatiotemporally with the progression of the outbreak, hydrodynamic conditions, and environmental degradation. The risk of infection transmission was estimated in the ambient water and between farms by the simulation of dispersal distances of infectious cohorts and farm connectivity. The impacts of farm locations on viral dispersal distance and connectivity levels were identified, which could provide valuable information for risk assessment and aquaculture management. Below, we discuss the capabilities of the model along with its limitations and possible future development.
4.1. Impacts of hydrodynamics on ISAV dispersal
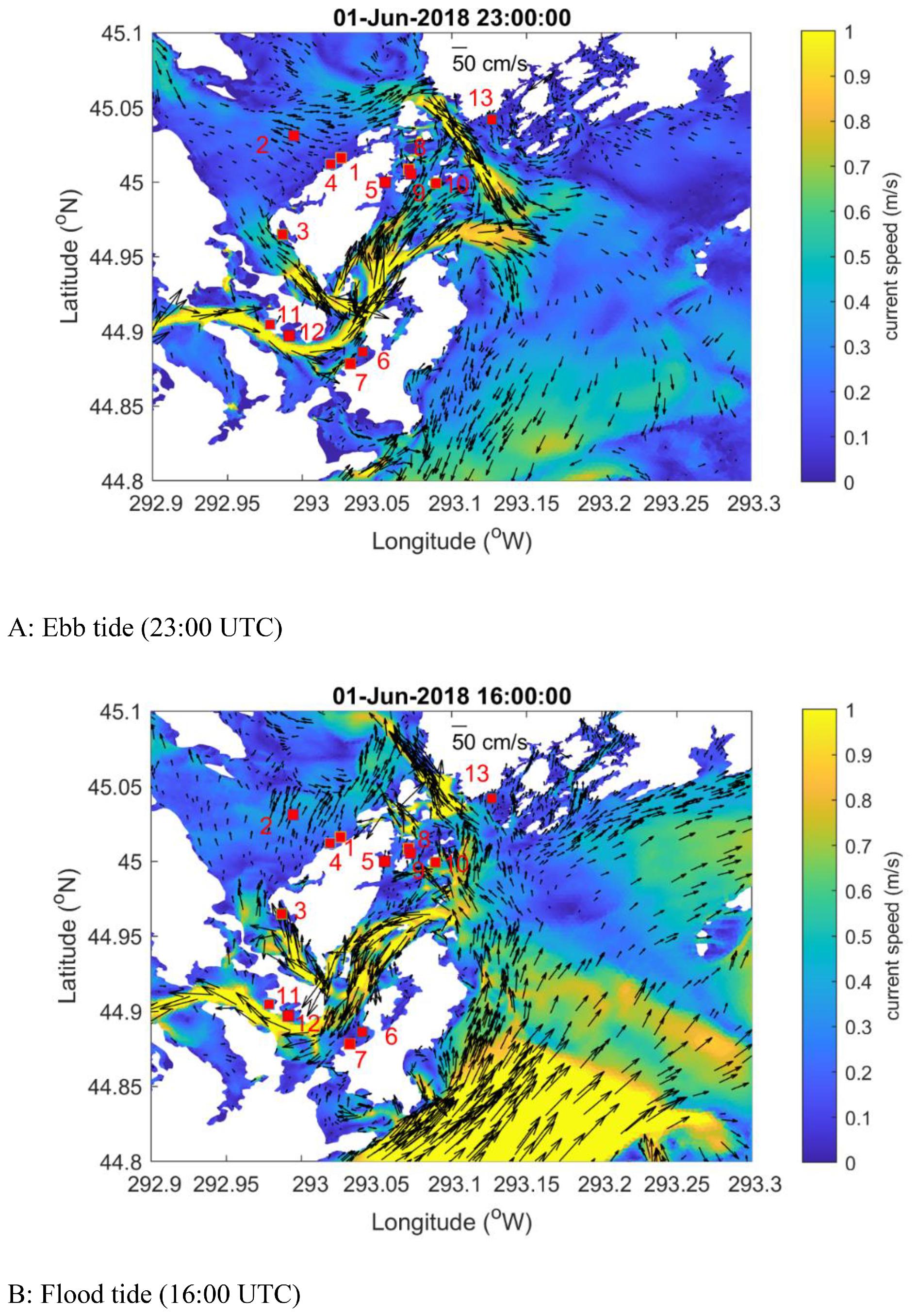
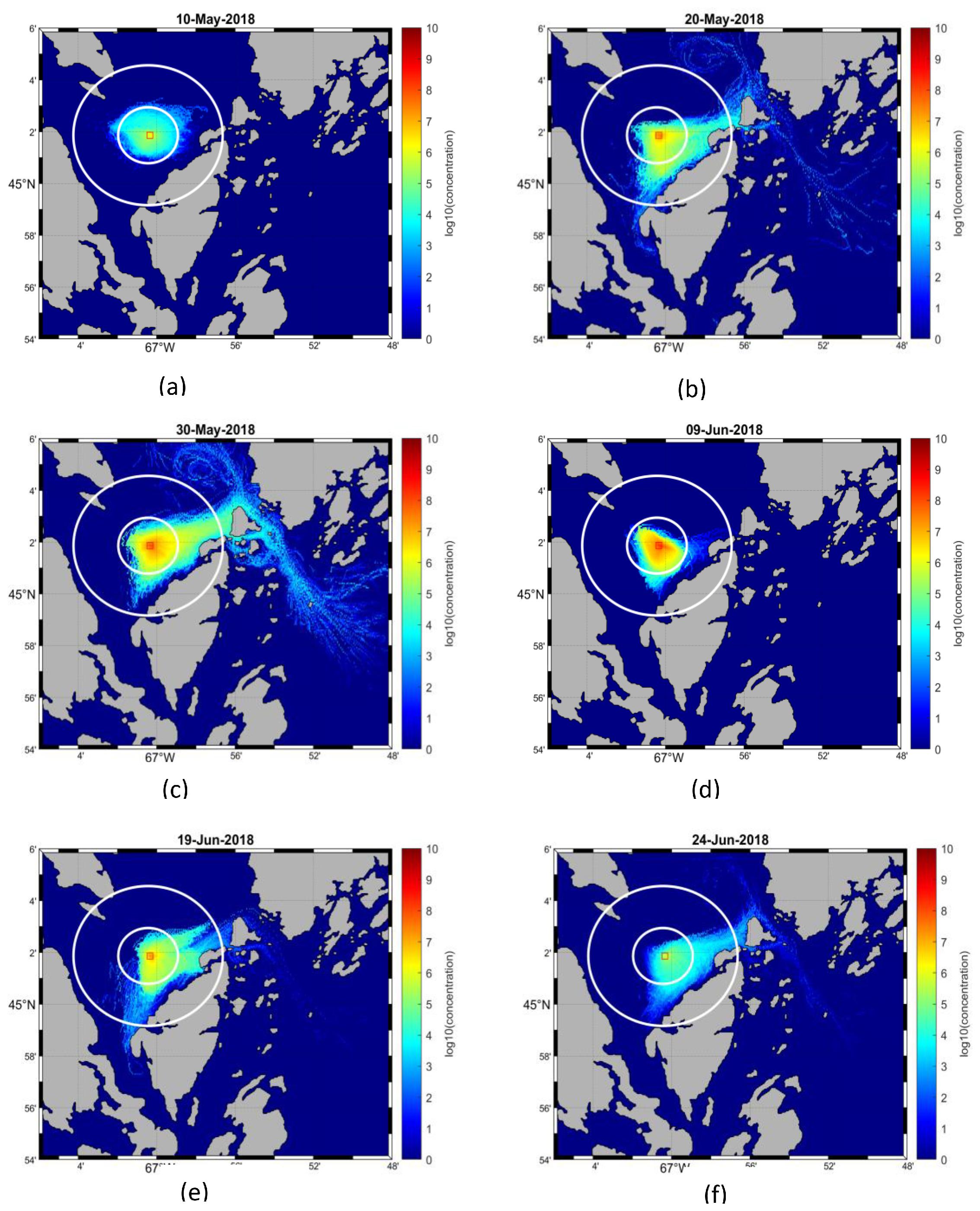
Since waterborne virus are expected to disperse passively, the physical movements of ISAV are substantially impacted by local hydrodynamic conditions. As a result, the spatial dispersion scales, as well as the concentration of ISAV, changed dramatically during the progression of the outbreak. For instance, while the viral concentration reached a peak around day 40, the dispersal scale was reduced markedly at that time instead of expanding. This change corresponded with the decreased tidal elevation amplitude at this time, modulated by the spring-neap tidal cycle, which was at a low level between days 35 and 40 post-outbreak (Supplementary Information 8). This indicates that, in tidally mixed systems, variation of tidal amplitude can be used to assist the prediction of viral dispersal, though many other factors also need to be considered, such as vertical mixing and turbidity caused by tidal dynamics (
Davies et al. 1995;
Pinon and Vialette 2018).
Current speeds are important for the dispersal distances of particles. As demonstrated in our results, particles from farms surrounded by high-speed currents had longer travel distances. In our simulations, the mean maximum dispersal distance of HVL cohorts was about 2.5 km for all selected farms, while it was about 6 km for Farm 6 as it is subjected to the fastest currents among the farms used in these simulations.
Page et al. (2005) estimated that the maximum displacement of modeled ISAV particles from salmon farms located along southern Grand Manan Island, NB, varied between 2.3 and 13.9 km on a single tidal excursion, depending on site. This was longer than what we obtained in our simulations, possibly because they did not account for the viral shedding dynamics and environmental decay in their simulations.
Our modeling results also indicated that the mean displacement of HVL cohorts was about 0.3 km from the studied farms, providing a preliminary reference for future field work on ISAV. Field studies conducted in Norway revealed that ISAV RNA could be detected within a farm site experiencing an ISAV outbreak, but not in downstream water samples collected 70-100 m away (
Løvdal and Enger 2002). This suggests that the dispersal of ISAV may be lower than predicted by our modeling effort. However, the number of infected fish, fish size, outbreak season, current speed and direction, and UV radiation condition were not reported in their study area, which can all impact the dispersion and concentration of ISAV dramatically, and need to be considered when comparing results among different ecosystems and seasons.
In our study, each farm was treated as a homogeneous unit, without considering the layout of individual cages and associated cage drag on hydrodynamics. In reality, farm areas are exposed to unique local oceanic conditions, as the flow speed and direction can be impacted by existing cage systems (
Wu et al. 2014,
2022;
Rickard 2020), which may affect viral dispersal. The viral transmission risk between cages likely varies as well, depending on the layout of cages (
Romero et al. 2021). Our assumption of a single unit could be improved by coupling the dynamics of infection between cages model developed by
Romero et al. (2021). Oceanographic conditions of hourly outputs from the FVCOM model were used to drive the particle tracking and reduce computing time of the simulations. Although this resolution has been generally used in tidally dominated areas (e.g.,
Foreman et al. 2015b;
Quinn et al. 2022), it may need to be refined. Notably, the stability of particle tracking results in relation to the frequency of the circulation model outputs should be validated further. In addition, the temporal resolution of the particle tracking module can impact the stability of the simulation as well and need to be considered. Our preliminary tests indicate that, within short tracking periods (e.g., 3 h), differences in particle trajectories between temporal steps of 30 s and 5 mins were relatively small (Supplementary Information 2). This indicates a limited impact of 30 s interval setting on our ISAV trajectories since viral lifespan is predicted to be short (i.e., <3 h).
The random walk scheme in the PTrack module includes smaller scale turbulent mixing with preset homogeneous horizontal and vertical diffusion coefficients. However, model outputs of the FVCOM suggest that in parts of our study area, vertical diffusion coefficients may be smaller than horizontal diffusion coefficients (Supplementary Information 4). A comparison of the particle trajectory performed using two different vertical diffusion coefficients showed that the dispersal scale of particles was larger when the vertical diffusion coefficient was set to 0.01 m
2 s
−1 compared to 0.1 m
2 s
−1. Considering that most of our selected farms are scattered in the higher vertical diffusion area based on the FVCOM estimation, a vertical diffusion coefficient of 0.1 m
2 s
−1 was used for this study, although vertical turbulences around farms 1, 2, 3, and 4 are likely much lower than for other farms. Introducing spatially variable vertical diffusion coefficients to the particle tracking model may improve the accuracy of particle trajectory simulations (
Stucchi et al. 2011).
4.2. Dynamic infection and viral shedding
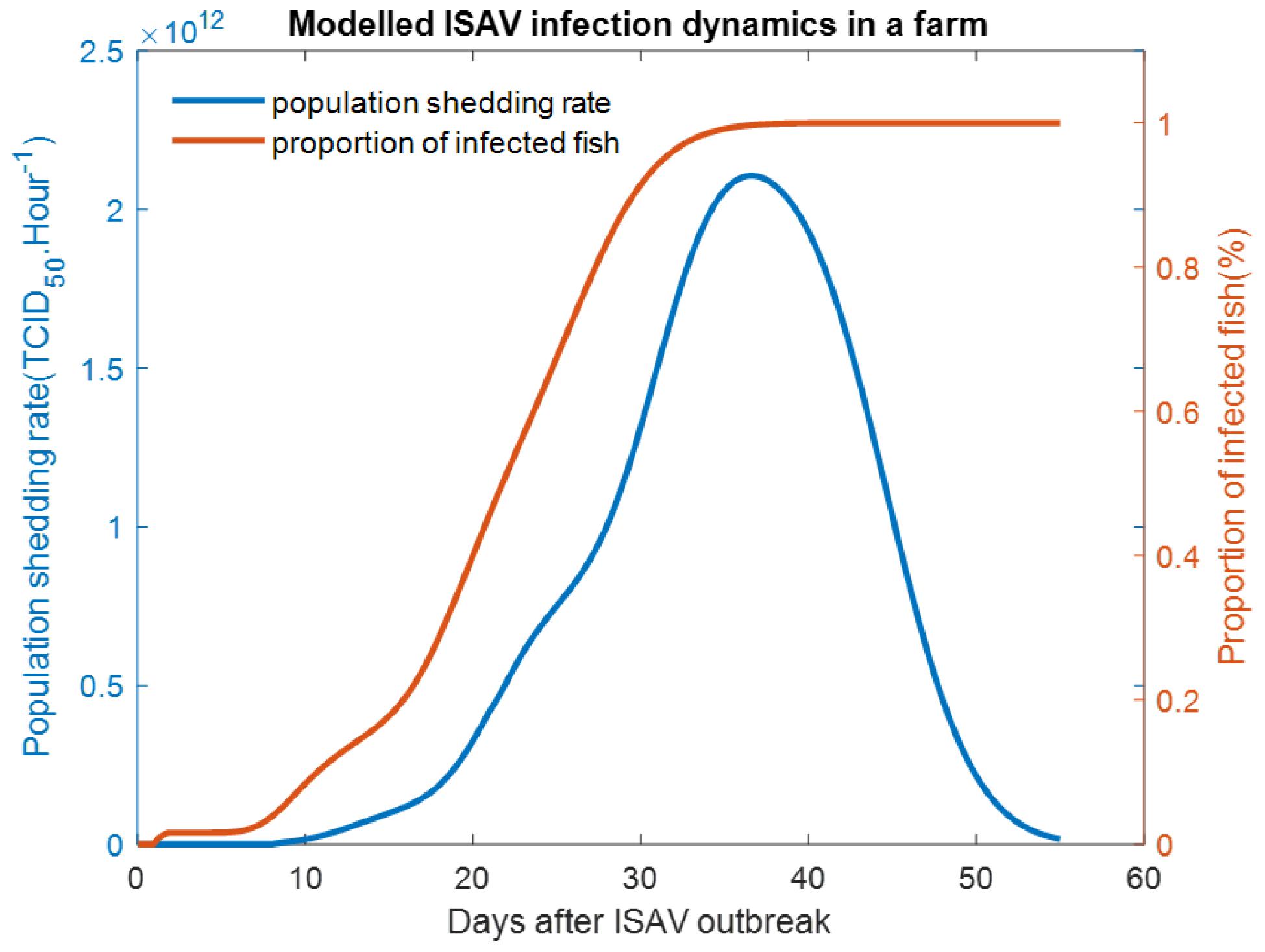
One key component of the current modelling framework is that it accounts for the progression of an infection within an index farm, which integrates factors including the number of susceptible fish, fish size, virulence of variants, prevalence of the initial infection, and shedding rates at any given time. These factors determine the amount of virus shed in surrounding waters throughout the outbreak, which directly impacts the dispersal predictions (
Salama and Murray 2011;
Foreman et al. 2015a,
2015b). These settings can be adjusted according to different scenarios, providing flexibility for the implementation of this framework. In our study, all the fish were assumed to be susceptible to ISAV, with an initial abundance set to 300 000 per site in all farms and an average fish weight of 5 kg (i.e., market size) to mimic a worst case scenario. In practice though, information on fish stocking and production cycles can be used to represent specific scenarios, and to harness the full potential of this framework for quantifying the role of fish density in ISAV transmission to neighboring farms and ambient water. For instance, fish are currently less than 200 g at the time of stocking in our study area. As such, ISAV outbreaks occurring in smaller fish would result in reduced viral concentrations shed into the water, resulting in a reduced risk of infection relative to the values estimated in the present simulations.
The transmission risk between fish is a stochastic process and user-determined parameter in this model, which can be modified in accordance with the virulence of different variants and environmental conditions (
Romero et al. 2021). The parameters used in this study to simulate the transmission risk of ISAV between fish were based on a beta-PERT (0.8, 0.9, and 0.99) distribution and represent a highly virulent scenario. This setting controls the entire outbreak time, which lasts for about 2 months in our simulation. The transmission risk may be lower than this for moderate variants, requiring different values for the beta-PERT function.
Estimating the shedding rate of ISAV-infected salmon is a complex task. Fish size, genetics, overall health status, temperature, and virus variants are all factors potentially influencing the virulence of the infection and the shedding rate (
Madetoja et al. 2000;
Hershberger et al. 2010;
Purcell et al. 2016). In addition, dead fish remaining at the bottom of the net pen could release ISAV for some time, though the infectivity of the viruses released by dead fish is unknown (
Wargo et al. 2017). In this study, fish were assumed to be removed once they were dead, and as such, dead fish did not release any ISAV in our simulations. The data we used to simulate individual shedding rates were extracted from the experimental work of
Gregory et al. (2009). Their results, obtained from a highly infectious ISAV variant, were based on polymerase chain reaction (PCR) detection of virus and converted to equivalent TCID 50 mL
−1 kg
−1 using a calibration curve. Since the quantification of RNA of ISAV does not discriminate between infectious virions and RNA (
Vike et al. 2014), the shedding rates used in this module may be overestimated. In addition, the
Gregory et al. (2009) did not specify if they accounted for the initial concentration of ISAV at the beginning of their shedding experiments, which could also lead to an overestimation of shedding rate. Hence, additional experiments would be beneficial to optimize the estimation of ISAV shedding rates.
In our current simulation, human interventions, such as vaccination and de-population, were not included, providing the perspective of a worst-case infection scenario. For highly virulent variants, management actions would likely be taken as soon as clinical signs and/or unusual rates of mortalities are observed, such as culling the fish. As a result, the actual outbreak time may be much shorter that was simulated in this study. The infection module can be adapted to include human interventions (
Romero et al. 2021), depending on the research purpose.
Exposure and infection resulting from multiple farm outbreaks were not accounted for in this study. During a disease outbreak, multiple farms can be infected and shed simultaneously, and this can have a cumulative impact. This scenario could be simulated using this framework with a few modifications.
4.3. Impacts of environmental parameters on ISAV inactivation
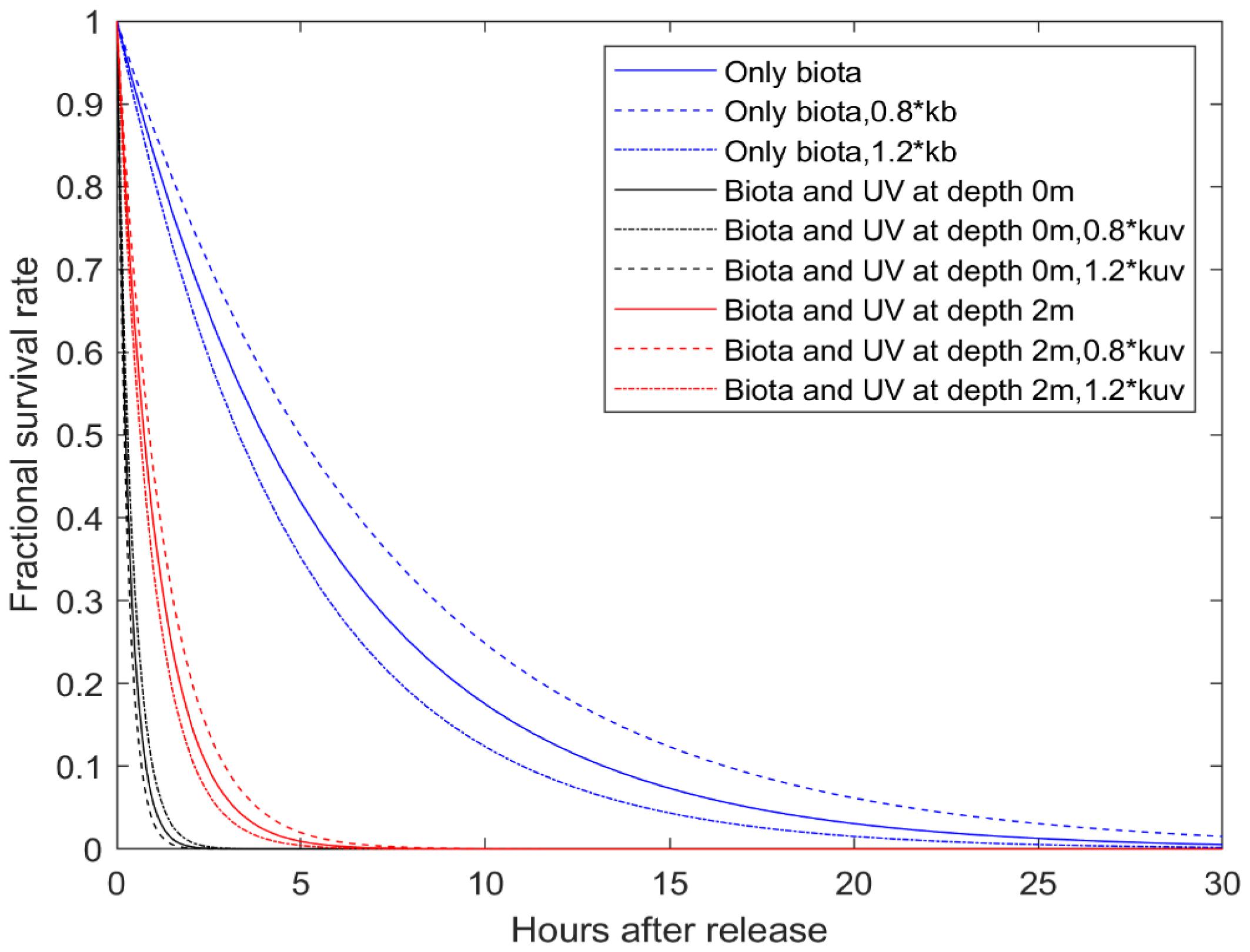
Waterborne viral cohorts are exposed to ambient seawater conditions that can affect their viability outside of the host, and, as a result, affect how far they can be dispersed by currents. In this study, we modelled the inactivation of ISAV in seawater as a function of both bacterial degradation and UV radiation. Sensitivity analyses indicated that the inactivation model was moderately sensitive to the uncertainty in these parameters; that is, a perturbation of ±20% changed the time to 99% inactivation time by about ±20% of the nominal value. Hence, there is a need to obtain accurate estimates of inactivation rates of ISAV along with the environmental conditions that are likely to affect these rates, such as UV radiation, to accurately predict the dispersal of ISAV in seawater.
In this study, we used the inactivation parameters that were derived by
Garver er al. (2013) for IHNV, assuming that the viability of ISAV was similarly affected by UV radiation and bacterial degradation. The model predicted that infectivity would decrease rapidly and be near zero after about 3 h. This is consistent with the results of laboratory studies performed using natural seawater that showed a near total loss of ISAV infectivity within 3 h following an exposure to ambient UV radiation (
Vike et al. 2014; D. Ditlecadet, unpublished data). In contrast, using sterilized water,
Nylund et al. (1994) reported a viral lifetime of 20 h for ISAV, suggesting that bacterial degradation of ISAV is significant in natural seawater. Consequently, virions apparently lose their infectivity within a relatively short timeframe, limiting the risk of transmission, as shown by our modelling results.
The model we used to estimate the effects of UV radiation on the viability of ISAV also requires measurements of UV radiation in the region where the modeling was conducted, as well as the UV attenuation coefficient with water depth. In this study, the UV index was from the city of Toronto (Canada), the closest operational UV monitoring station. The relatively higher latitude of the Quoddy Region is expected to correspond to a lower UV index than Toronto, especially in the summer, when a 3% difference can exist during May to June, according to the numerical forecast data from Environment and Climate Change Canada (
https://exp-studies.tor.ec.gc.ca/). Hence, the UV radiation used in our simulation may have been overestimated by approximately 3%. For the UV attenuation coefficient with water depth, we used the value derived by
Foreman et al. (2015b) based on measurements conducted in the Discovery Islands, British Columbia. In addition, differences in cloud coverage between regions were not accounted in the present analyses, which could have biased the level of UV radiation predicted to reach the surface of water. UV attenuation rate with water depth is heavily modulated by the dissolved organic matter (DOM) content, sedimentation, and plankton concentration of the water, which themselves have strong spatial and seasonal variations (
Häder et al. 2015). The interaction of these impacts may change the dispersal of ISAV, adding uncertainties to the modelling results. Obtaining UV measurements and attenuation coefficient for the studied area that also accounts for regional variation in cloud coverage would greatly reduce uncertainty, resulting in a more robust model.
The inactivation module can be adapted to account for additional environmental factors that may affect the viability of viruses, such as water temperature and salinity (
Tapia et al. 2013). In our study, the inactivity coefficients derived at 10 °C was adopted (
Garver et al. 2013). We did not account for changes in water temperature, which varied between 7 and 10 °C over the course of our simulation, though the viability of ISAV was expected to vary by less than 8% over that range of water temperatures (
Tapia et al. 2013). Nevertheless, further effort is required to model the effect of water temperature and other environmental conditions on the viability of ISAV in local water.
4.4. Farm connectivity and aquaculture management
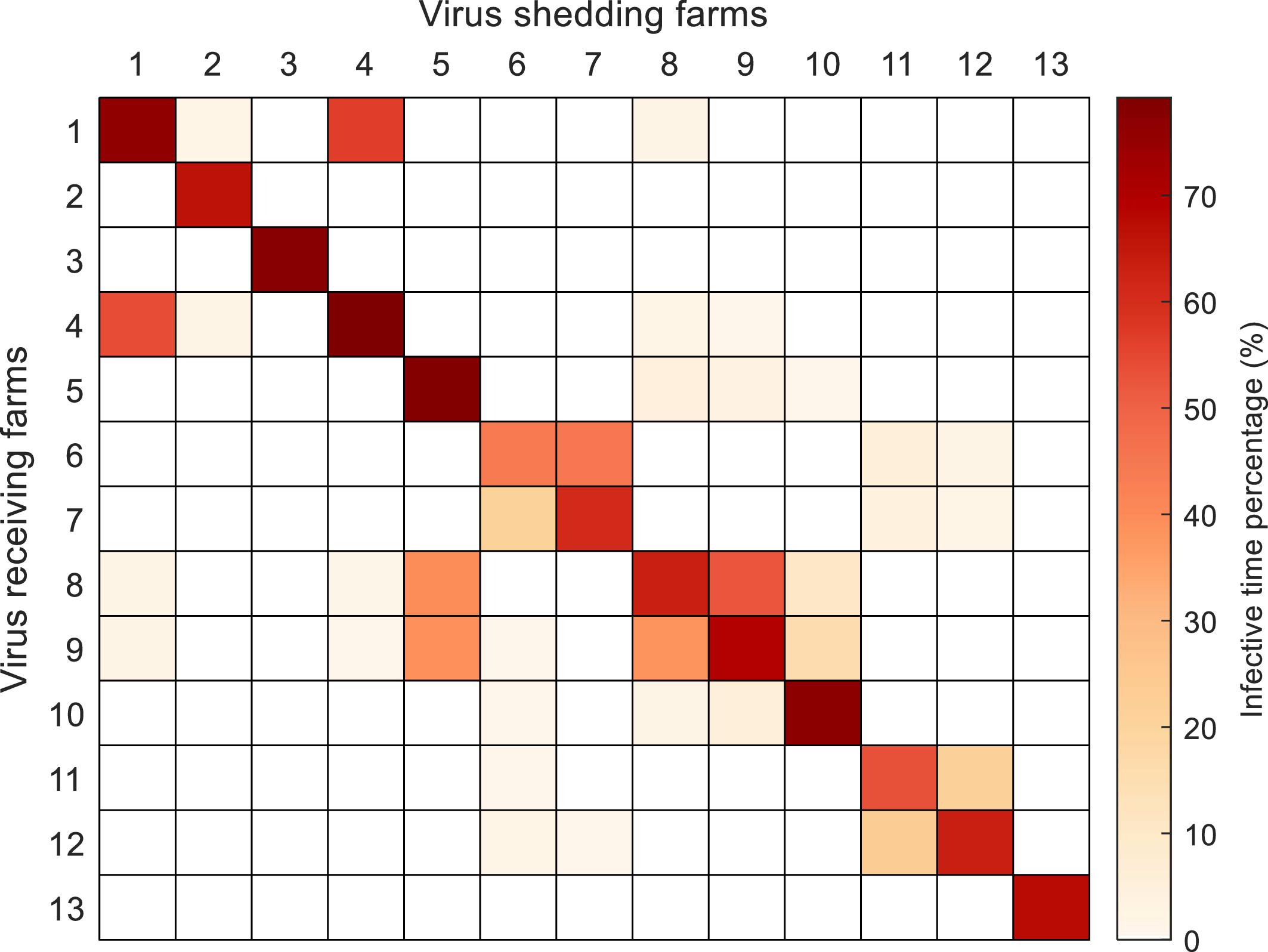
Connectivity analysis is useful to identify which sites have a higher potential of affecting other sites. Our simulations indicate that the potential for connectivity risks between several close farms could be higher than 50%. Without efficient early stage disease surveillance and response, infection transmissions are likely to occur among these farms. This supports the importance of industry adherence to stringent surveillance programs and disease management practices to minimize risks to nearby farms and wild species (
NBDAAF 2020). Meanwhile, it should be noted that the dynamics of the outbreak and shedding rate may vary with the ISAV variants based on their virulence. For infections induced by highly virulent ISAV variants, actions are usually taken in earlier stages to reduce the risk of transmission between farms, and their impact.
Seaway distance has frequently been used in previous studies to estimate the connectivity among farms (
Aldrin et al. 2011;
Gautam et al. 2018;
Parent et al. 2021). Our results indicate that accounting for seaway distance is essential when predicting connectivity between farms, given that most farms separated by short seaway distances showed high potential infectious connectivity. However, our connectivity and current vectors analyses indicate that it is also important to consider current directions due to the asymmetrical connectivity between some farms. For instance, we show that Farm 5 likely had a significant impact on Farms 8 and 9, while the reverse was less probable. These results further highlight the importance of considering ocean circulation to understand viral transmission and connectivity among farms rather than just distance alone (
Gustafsen et al. 2007;
Foreman et al. 2015b), supporting previous findings that farm location can play a vital role in disease transmission (
Page et al. 2005).
The modelling results also indicated that the two farms located in Cobscook Bay, Maine, were connected to several farms located in Canadian waters, though at a very low level. This is a reminder that what happens in one jurisdiction might affect salmon farms in other jurisdictions and emphasizes the importance of bilateral coordinated efforts to improve aquaculture management.
In addition, modeling the connectivity between farms may provide some insight into the flushing ability of the index farm, as the diagonal line of that matrix is an indicator of the retention time of infectious particles at those sites. As the shedding dynamics were the same for all farms in our simulation, farms with high flushing ability can flush away the infectious particles in a relatively brief time, resulting in a reduced retention probability. For instance, Farm 6 had the lowest retention time, and dispersal distance of HVL particles from Farm 6 was the longest among the 13 farms. Such information can be useful to study the local environmental impacts of aquaculture activities, such as dispersion and deposition of fish feces and leftover food (
Law and Hill 2019).
4.5. Future perspectives
It is always challenging to measure virus transmission in a real and dynamic marine environment due to the difficulty of conducting a large-scale field survey at the time of a virus outbreak. The current modelling framework provides a useful tool to understand such processes. The modelling results can be further validated and improved by integrating results of more laboratory and field work, including spatial epidemiological data, e.g., eDNA sampling and detection of pathogens and parasites in water samples, at a regional scale (
Abbott et al. 2021).
By coupling the infection dynamics with other modules, this framework allows scenarios of outbreaks at earlier and later infection stages, as well as such management interventions, like culling and vaccination, to be simulated independently. Seasonal variations can be estimated by simulating outbreaks occurring at different times, especially with more environmental parameters involved. The spatial and temporal distribution of virus can also be simulated with this framework, allowing us to estimate the potential of infection in an area following one or multiple outbreaks. This is a key component to assess the risk of ISAV transmission not only to other farms, but also to wild Atlantic salmon that may transit through these sites. For instance, the migration paths and swimming behavior of Atlantic Salmon post-smolts were studied in the area where we simulated the dispersal of ISAV in this study (
Lacroix et al. 2004;
Quinn et al. 2022). With such information, this framework can be applied to estimate the potential exposure of wild fish to ISAV and assess the risk of farm-to-wild fish disease transmission.
The connectivity matrix obtained in this study may also prove to be a valuable tool for management purposes to guide site location and deployment of monitoring resources, as was done for sea lice in Scotland (
Adams et al. 2016). For instance, the creation of BMAs in southwest New Brunswick was implemented in 2005 as part of the efforts to control ISAV in this area (
Page et al. 2005, F. Page personal communication). Although the models used at the time to define these areas were relatively simple (i.e., an M2 (semidiurnal lunar tidal constituent) circulation model, ballpark estimates of viral inactivation time scales, no consideration of time-dependent shedding), the estimated displacement scales were considered reasonable and somewhat precautionary estimates for the geographic area based on the limited data available at the time. It was also recognized that the exchange of viral loads between farms within each BMA would likely occur to varying degrees, but that exchanges between BMAs were expected to be much more limited (F. Page, personal communication). Our preliminary assessment of the connectivity between those BMAs based on a limited number of farms appears to support these delineations. For instance, Farms 1 to 10 in BMA1 were not connected to Farm 13 in BMA2 in our simulations. Further work is required to fully assess the effectiveness of these BMAs for ISAV and other pathogens and parasites, such as sea lice.
We acknowledge that the assumptions used in this framework, and their associated limitations, both individually and in combination, introduce potentially large uncertainties in the simulated values. This framework should be viewed as a baseline to future refinements and provide some guidance for managing the relative risk of waterborne ISAV and other pathogens’ transmission.