Introduction
The weathering of carbonate and silicate rocks on land is a key process in the global carbon cycle and, through its coupling with calcium carbonate deposition in the ocean, is the primary sink of carbon on geological timescales (
Urey 1952;
Walker et al. 1981). The rate at which these processes remove carbon from the Earth system is sensitive to changes in the environment, notably temperature (
Berner 1991), biological production (
Lenton and Britton 2006), and perhaps more indirectly, river runoff (
Walker and Kasting 1992). This gives rise to a negative feedback mechanism that regulates the global climate on multimillennial timescales. However, there have been very few quantitative assessments of its impacts on carbon cycling and ocean biogeochemistry, and its relevance over time frames of 10
4 years or shorter is largely unknown.
The purpose of this paper is to investigate how the potential changes in global terrestrial weathering may have affected ocean biogeochemistry and the global carbon cycle during the last deglacial period (∼19 000–4000 BC). Changes in weathering rates are expressed as a modulation of initial conditions based on changes in temperature, atmospheric CO2, or vegetation net primary production (NPP), and various parameterizations are tested and compared using the University of Victoria Earth System Climate Model (UVic ESCM). A prescribed time series of atmospheric CO2 is used to accurately drive climate change during the period and thus better estimate changes in weathering rates. The impact of the latter on atmospheric CO2 concentrations is then determined using the weathering rates obtained previously as boundary conditions for a second set of simulations performed at various periods of the deglaciation during which atmospheric CO2 is allowed to vary according to model carbon cycle dynamics. Overall, this study allows us to make an estimate of the variations in weathering rates within glacial–interglacial timescales and their impact on the carbon cycle.
The chemical weathering of rocks is characterized by the cleavage of bonds of the mineral lattice by water, often in the presence of an organic or inorganic acid. Carbonic acid (H
2CO
3) is one such secondary weathering agent, acquired from the dissolution in rainwater of atmospheric carbon or the oxic degradation of organic matter in soils. Rock weathering products, including calcium and bicarbonate ions (the most abundant cation and anion, respectively, in most river waters), can be carried away with runoff to rivers and into the ocean. For example, calcium carbonate dissolution by carbonic acid is represented by:
The influx of dissolved inorganic carbon (DIC) ([CO
2(aq)] + [H
2CO
3] + [HCO
3 −] + [CO
3 2−]) and carbonate alkalinity (CA) ([HCO
3 −] + 2[CO
3 2−]) to the ocean surface layer is balanced by the precipitation and burial of biogenic calcium carbonate (CaCO
3) in the marine sediments; perturbations to the oceanic [CO
3 2−] (= (DIC − CA) at the pH of seawater) result in a repositioning of the carbonate compensation depth (CCD), the depth below which the dissolution rate of calcium carbonate exceeds its flux to the deep sea. In the long term, this allows the ocean to maintain a remarkably stable alkalinity, as any increases in ocean acidity (such as can be caused by a CO
2 invasion from the atmosphere) can be neutralized by elevating the CCD, exposing carbonate sediments to dissolution, and the release of carbonate ions (CO
3 2−) back into the ocean. This oceanic buffer factor, along with carbonate dissolution on land (due to weathering), is the primary means through which ocean alkalinity is restored and is responsible for maintaining both atmospheric and oceanic pCO
2 close to equilibrium. In short, the weathering of calcium carbonate can accelerate the transfer of CO
2 between the atmosphere and the ocean, but it does not contribute to a permanent return of carbon to the geologic reservoir (
Ridgwell and Zeebe 2005;
Sarmiento and Gruber 2006).
A large fraction of rock weathering reactions involves a weakening of chemical bonds in the lattice of silicate minerals on contact with water, whereby hydrogen ions replace positively charged cations (mostly Ca
2+ and Mg
2+), which are bounded to the negatively charged ion (alumino)silicate framework. One of the most common examples is given by calcium silicate hydrolysis, as described by the following schematic, irreversible (at Earth surface conditions) reaction (
Ebelmen 1845;
Urey 1952):
This equation represents the weathering of a simple silicate mineral (in our example, wollastonite) into silicic acid (which often precipitates as amorphous silica SiO
2), consuming one more molecule of CO
2 than carbonate dissolution while sending the same amounts of calcium and bicarbonate ions to the ocean. The combination of
eq. (2) with calcium carbonate precipitation (the reverse of
eq. 1) shows how this results in a net removal of one molecule of CO
2:
Weathering rates due to silicate hydrolysis tend to be considerably slower than from the dissolution of carbonate minerals—it removes on an average of 0.28–0.30 Pg C per year (
Amiotte Suchet and Probst 1995)—hence, the effect of atmospheric CO
2 consumption by silicate weathering only becomes a significant sink of carbon on geological timescales (10
5 to 10
6+ years). For the remainder of this article, dissolution of carbonates (on land) and hydrolysis of silicates will be treated separately and referred to as carbonate and silicate weathering, respectively.
The role of rock weathering in regulating long-term global climate has been established by past box-modeling efforts (
Walker et al. 1981;
Berner et al. 1983;
Berner 1991). These studies linked the rate of atmospheric CO
2 consumption by silicate weathering to changes in atmospheric partial CO
2 pressure, as a possible explanation for the general decreasing trend of atmospheric CO
2 levels on geological timescales. Although atmospheric CO
2 concentration is often used as a broad proxy for environmental and(or) climate change, sometimes the direct effects of temperature and river runoff were also parameterized in these studies.
Walker et al. (1981) (commonly referred to as WHAK) developed expressions relating silicate weathering to atmospheric pCO
2 (through vegetation production) and temperature (including a weak dependency on runoff) and used them to offer a solution to the faint young Sun paradox by providing a convenient mechanism for a slow and steady decrease in atmospheric greenhouse gas concentrations. Although the model used rudimentary parameterizations derived from early general circulation models and experimental data, it built a foundation for future long-term carbon cycle model studies.
Berner et al. (1983) (commonly referred to as BLAG) built a geochemical cycle model in which the long-term evolution of atmospheric carbon content is driven by imbalances between CO
2 outgassing by volcanic activity and the burial of carbonate sediments that follows the weathering of silicate rocks. In this model, the silicate weathering rate was given a similar dependency on temperature and atmospheric CO
2, and it was used to solve a series of mass balance equations to determine the inward and outward fluxes for the atmospheric, land, ocean, and mineralogical carbon reservoirs. Following
Berner et al. (1983),
Berner (1991) simplified the geochemical component by lumping together the carbonate minerals and combining the atmosphere and ocean into a single reservoir, in favor of adding more direct biological mechanisms (notably, the soil-biological enhancement of weathering). Land area, elevation, and runoff were also introduced as parameters in the new model called GEOCARB. Much like its predecessor, this model was developed to reconstruct the evolution of atmospheric pCO
2 over the past hundreds of millions of years (which was calculated as a series of successive atmosphere–ocean steady states). Subsequent versions were called GEOCARB II (
Berner 1994) and GEOCARB III (
Berner and Kothavala 2001), and these further improved the weathering parameterizations based on the latest observational data and global circulation model (GCM) output.
The importance of the negative feedback mechanism associated with rock weathering is somewhat underwhelming on non-geological timescales, with few notable exceptions; chief among these is the late Pleistocene epoch (
Kump and Alley 1994;
Munhoven 2002) because of the rapid climatic and environmental changes that accompany glacial inception and termination. Yet, due to a lack of a quantitative assessment of the latter’s impacts on global rock weathering, there is considerable uncertainty as to whether the intensity of each glacial or interglacial period would be reinforced or tempered as a result of changes in weathering rates (
Bluth and Kump 1994). On the one hand, the combination of cooler global temperatures and weathering-inhibiting ice sheets should act to reduce CO
2 consumption from chemical weathering during glacial maxima, hence keeping with its perceived role as a negative feedback mechanism. On the other hand, the drop in mean sea level during said glaciations would have increased the effective area of continental shelves that are exposed to weathering, including a large increase in continental land area at low latitudes. Moreover, the intense pressure of ice sheets could increase the mineral reactivity of silicate rocks, thus drastically increasing weathering rates for a short period when the ice sheet retreats and the area is subject to weathering again (
Kump and Alley 1994). However, little is known about the relative impacts of each of those factors; thus, it is difficult to establish with certainty what would have been the role of rock weathering in the context of shifting glacial conditions in the northern hemisphere.
Few attempts have been made using climate models to investigate the significance of variations in chemical weathering rates during the Pleistocene glacial cycles.
Bluth and Kump (1994) developed a spatially explicit, empirical weathering scheme in which the runoff dependency of weathering is modulated by the local lithological composition. Considering an increase of continental margins and a decrease in ice-free continental land during the last glacial maximum (LGM), this model could not reproduce the apparent increase in global silicate weathering that was suggested by the Ge/Sr isotope records of that time (
Gibbs and Kump 1994). In an intercomparison study,
Munhoven (2002) compared glacial–interglacial variations in CO
2 between the latter and the GEM-CO
2 (
Amiotte Suchet and Probst 1995) models. Glacial bicarbonate production rates were found to be 20%–30% lower compared with the present day, whereas CO
2 consumption rates decreased by 5%–20% during the LGM, accounting for up to one quarter of the total fluctuations in atmospheric CO
2 levels. The loss in CO
2 consumption was not partitioned equally between the two weathering processes, with a slight increase in modern silicate weathering being accompanied by a much larger decrease in carbonate weathering. More recently, the importance of rock weathering on glacial timescales has been questioned;
Foster and Vance (2006) argued that the reduction of weathering in glaciated continental interiors would have been significant enough to negate the enhancing effect of exposed continental shelves due to receding sea levels.
The remainder of this paper is divided into four sections. The first section describes the climate model used in this study, and the second section presents an overview of the experimental setup. The “Results” section presents the outputs of the transient and snapshot model runs. Concluding remarks are given in the final section.
Model description
This study uses version 2.9 of the University of Victoria Earth System Climate Model (henceforth UVic ESCM), which is an intermediate-complexity coupled atmosphere/ocean/sea-ice model with integrated land surface and vegetation schemes (
Weaver et al. 2001). Its main component is version 2.2 of the Geophysical Fluid Dynamics Laboratory (GFDL) modular ocean model (MOM), a three-dimensional ocean general circulation model with 19 uneven vertical levels (
Pacanowski 1995), which is coupled to a vertically integrated energy–moisture balance atmosphere model (
Fanning and Weaver 1996), a dynamic–thermodynamic sea-ice model (
Bitz et al. 2001), a land surface scheme and dynamic global vegetation model (
Meissner et al. 2003), and a sedimentation model (
Archer 1996). Land surface properties (surface temperature, soil moisture content and temperature, and snow cover) and soil carbon content are computed with a single (1 m) layer version of the Meteorological Office surface exchange scheme version 2 (MOSES-2) (
Cox et al. 1999), and terrestrial vegetation dynamics are handled by the Hadley Centre’s top-down representation of interactive foliage and flora including dynamics (TRIFFID) model (
Cox 2001). The TRIFFID model describes the state of the terrestrial biosphere in terms of soil carbon content and vegetation distribution, which is expressed through the structure and coverage of five plant functional types: broadleaf tree, needleleaf tree, C
3 grass, C
4 grass, and shrub vegetation.
The model is driven in the short term by seasonal variations in solar insolation and wind fields (
Kalnay et al. 1996) and in the long term by orbital parameter changes and a reconstruction of atmospheric CO
2 content over the past 20 000 years (
Indermühle et al. 1999). The spatial coverage and height of continental ice sheets, which are prescribed every 1000 years using data from the model ICE-5G (
Peltier 2004), also act as a driver of climate change during the deglacial period. The land–sea configuration used in all subcomponents operates in a global spatial domain with a spherical grid resolution of 3.6° (zonal) by 1.8° (meridional), which is comparable with most coupled coarse resolution atmospheric-oceanic global circulation models (AOGCMs). In the current configuration of the model, ocean bathymetry and sea level are static and fixed to present-day conditions, and thus some features of the LGM and deglacial period are not included here, such as the lower sea level and appearance of continental shelves in shallow portions of the current-day ocean.
Terrestrial weathering in the UVic ESCM is parameterized as a land-to-ocean flux of dissolved inorganic carbon (F
DIC) and alkalinity (F
ALK, with F
ALK = 2F
DIC) via river discharge. In the standard version of the model, the incoming flux of carbon to the ocean as weathering is set to equal the sedimentation rate of CaCO
3 to balance the long-term carbon and alkalinity budgets in the ocean; the initial, steady-state value is typically held constant throughout the transient model runs. This effectively suppresses the long-term negative feedback mechanism by preventing the weathering rate from adapting to changes in environmental factors such as temperature and atmospheric CO
2 concentration.
Meissner et al. (2012) replaced the standard parameterization of weathering in the UVic ESCM with a number of adaptations from previous carbon-cycle box-models (see “Methods” section) to introduce and investigate the weathering negative feedback mechanism in the context of
future climate change scenarios. They found that the long-term climate response to various emission scenarios depends almost exclusively on the total amount of CO
2 released, regardless of the rate at which it is being emitted, and that carbon uptake through an increase in terrestrial weathering has a significant effect on the climate system. There were, however, some differences between the various weathering schemes concerning the rate of carbon removal.
Methods
In this study, we investigated the variation in rock weathering rate during the last deglacial period (16 000–4000 BCE) using a box-model approach whereby we modulated the initial global weathering following changes to certain parameters: globally averaged surface air temperature (SAT), globally averaged atmospheric carbon dioxide (CO
2) concentration, and globally summed vegetation NPP. Our objective was to assess the potential impacts of deglacial climate change on the long-term carbon cycle, notably through the changes in global chemical erosion rates and their effects on atmospheric carbon dioxide concentrations. To this end, various parameterizations of carbonate and silicate weathering were adapted to the UVic ESCM to examine the scope of possible climate and carbon cycle responses. One model version called GEOCARB followed the parameterization introduced in GEOCARB II (
Berner 1994) and subsequently used in GEOCARB III (
Berner and Kothavala 2001), which expresses the flux of weathering as a function of changes in temperature and atmospheric CO
2:
where
and
F Alk,w,0 and F
DIC,w,0 are the LGM riverine flux of alkalinity and dissolved inorganic carbon (DIC),
pCO
2 is the atmospheric CO
2 concentration, SAT is the global mean SAT, and the index 0 denotes the initial state (i.e., LGM) values. The factors
f Si and
f Ca stand for fraction of silicate (0.25) and carbonate (0.75) weathering, respectively (
Lenton and Britton 2006). An adaptation of the GEOCARB models proposed by
Lenton and Britton (2006), in which atmospheric CO
2 is replaced with the more variable vegetation NPP rather than atmospheric CO
2, served as a second model version that we will refer to as LB:
where NPP is the global mean net primary production. Our third version was based on an alternative formulation by
Uchikawa and Zeebe (2008), henceforth UZ, which loosely follows
Walker and Kasting (1992) in calculating variations in global weathering intensity as a sole factor of atmospheric CO
2 content:
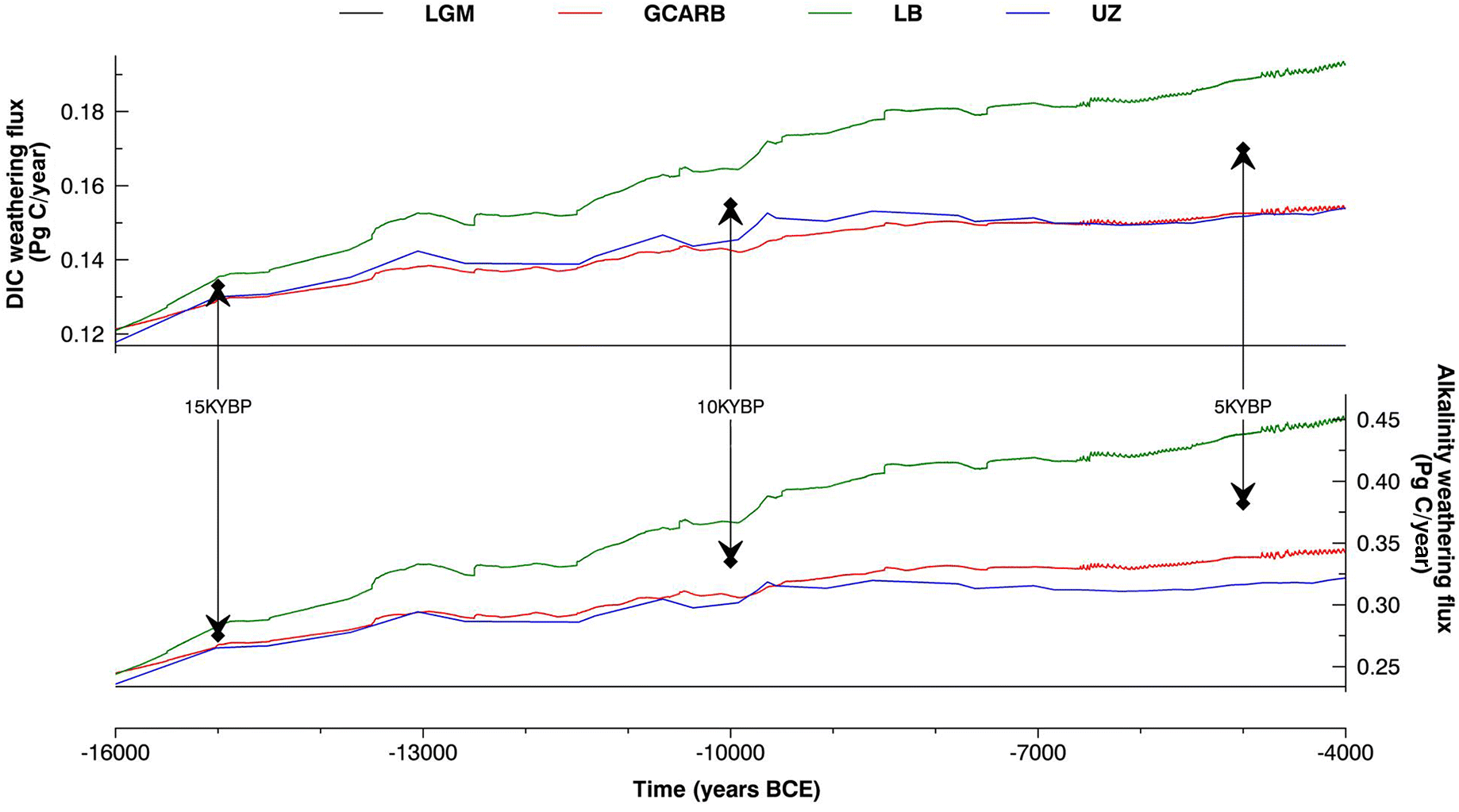
Finally, our fourth parameterization, called LGM, used fluxes of DIC and alkalinity which remained constant at their LGM value (F Alk,w = F Alk,w,0; F DIC,w = F DIC,w,0).
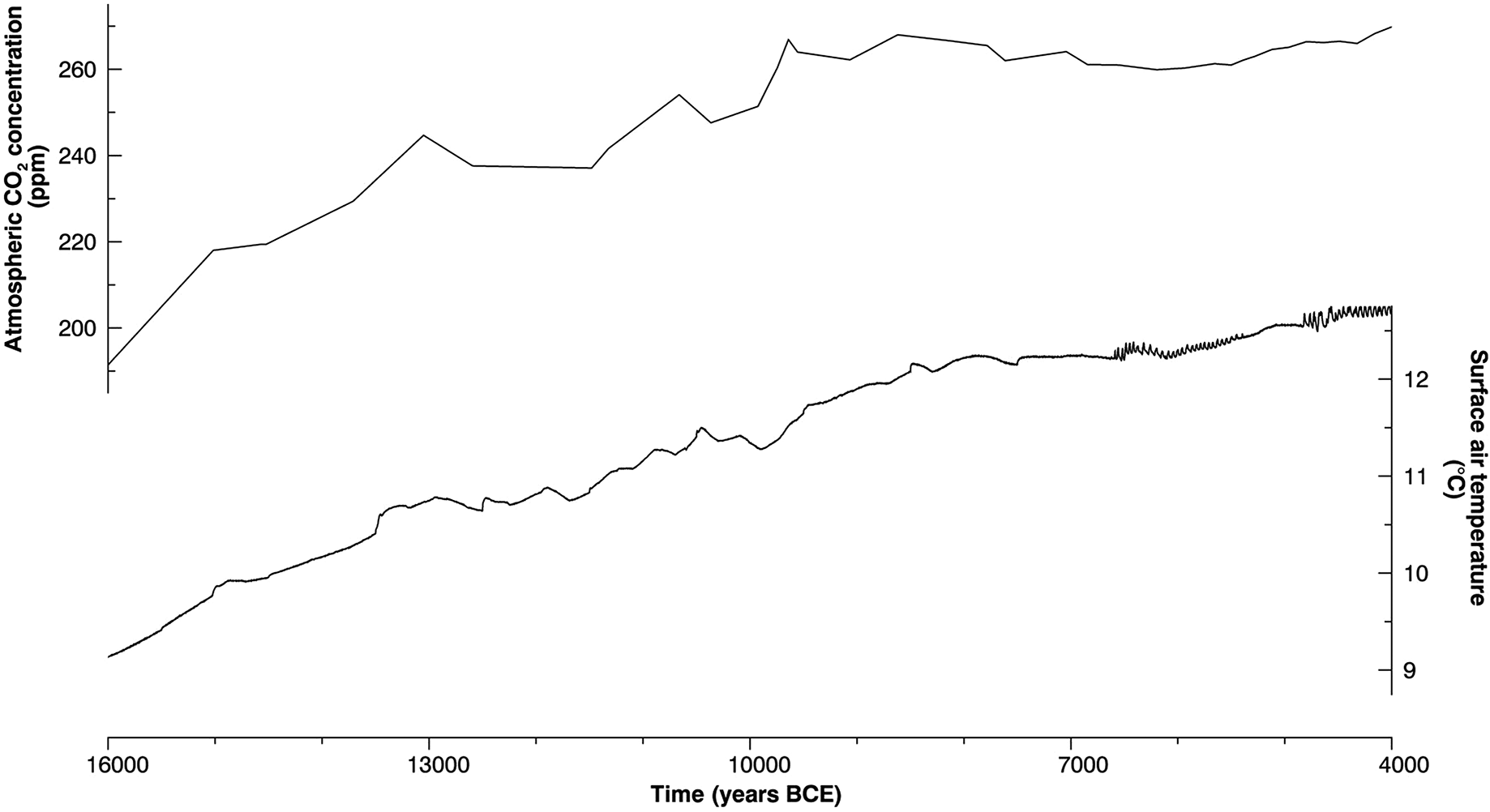
It is important to emphasize that these box-model parameterizations were taken out of their original, pre-industrial contextual frame, and applied to LGM and deglacial conditions. Initial temperature and NPP were calculated from a 10 000+ year equilibrium run with LGM (19 000 BCE) boundary conditions. LGM values for globally averaged temperature (9.15 °C), globally summed NPP (39.3 Pg/year), as well as weathering fluxes of DIC (0.12 Pg C/year) and alkalinity (0.24 Pg C/year) were in reasonable agreement with previous estimates of glacial conditions (
Bluth and Kump 1994;
Brovkin et al. 2012). The simulated glacial weathering DIC and alkalinity fluxes were somewhat lower than in other models; this discrepancy is mainly caused by the absence of LGM continental shelves in this version of the model, which causes it to underestimate the global rate of carbonate weathering. Variations in atmospheric CO
2 levels were prescribed based on ice core data from the Taylor Dome in Antarctica (
Indermühle et al. 1999), and acted as the main driver of deglacial climate change alongside prescribed continental ice sheet retreat (
Peltier 2004) and astronomical changes in solar insolation (
Berger 1978). Starting from LGM equilibrium values, the UVic ESCM was integrated to year 4000 BC (totaling 15 000 years) for each of the four weathering parameterizations described above. Results are presented in the “Ocean biogeochemistry” subsection.
The reasoning behind our prescribing of atmospheric CO
2 content lies in the inability of the UVic ESCM to reproduce the observed trend of CO
2 during the deglacial period and early Holocene (
Simmons et al. 2016). One of the major restrictions of this approach, however, is that it prevents assessing the direct response of atmospheric CO
2 content to changes in global weathering intensity, effectively limiting the investigation to changes in ocean biogeochemistry, notably the DIC and alkalinity content of the ocean. Hence, we devised a second set of experiments whereby fixed DIC and alkalinity weathering fluxes would be used to estimate potential changes in atmospheric CO
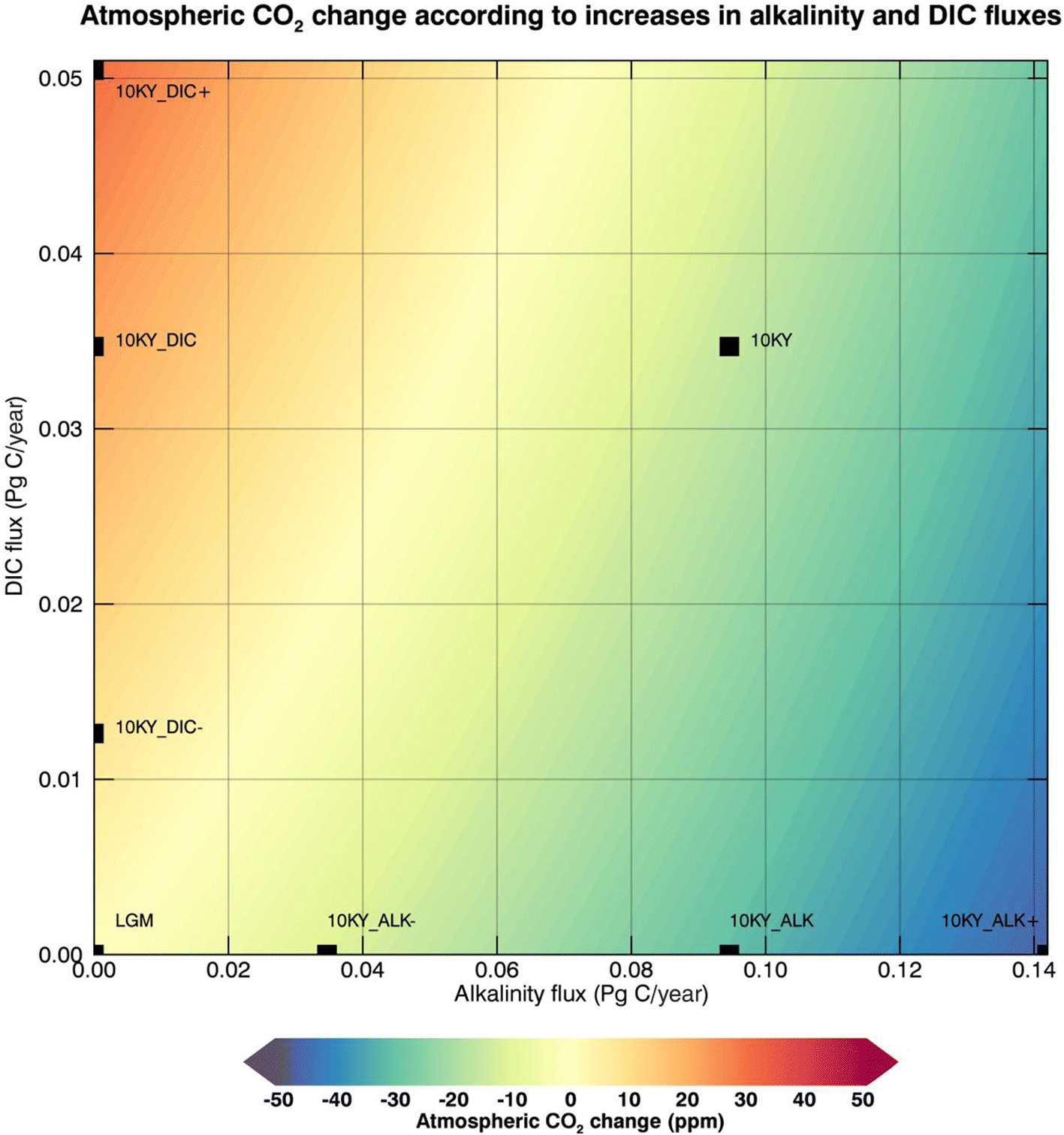
2 within long-term equilibrium run under appropriate boundary conditions (ice sheet distribution and orbital parameters). The model was first spun up with 10 000 BCE and 15 000 BCE conditions and LGM (aka. 19 000 BCE) weathering fluxes. Then, for each respective time period, the values of those fluxes were increased by predetermined amounts (see
Table 1), and the model was integrated for several thousand years for each set of DIC flux and alkalinity flux values. A total of 12 simulations were integrated and compared (see
Table 1). This set of experiments, described in greater detail in the “Changes in atmospheric CO
2” subsection of the Results, allowed us to explore the sensitivity of the atmospheric CO
2 response to the respective changes in weathering DIC and alkalinity fluxes as well as the changes in this sensitivity through different stages of the deglacial period.
Conclusions
In this paper, we examined the effect of deglacial weathering changes on ocean biogeochemistry and atmospheric CO
2 using a set of box-model parameterizations of weathering fluxes within the UVic ESCM. We used weathering parameterizations based on temperature (
Berner 1994), atmospheric CO
2 concentrations (
Walker and Kasting 1992;
Uchikawa and Zeebe 2008), and vegetation production (
Lenton and Britton 2006), first adapted to the model by
Meissner et al. (2012), to diagnose the change in riverine alkalinity and DIC fluxes during the latest deglacial period. The model was run from the end of the LGM (16 000 BCE) to the mid-Holocene (4000 BCE) using prescribed changes in atmospheric CO
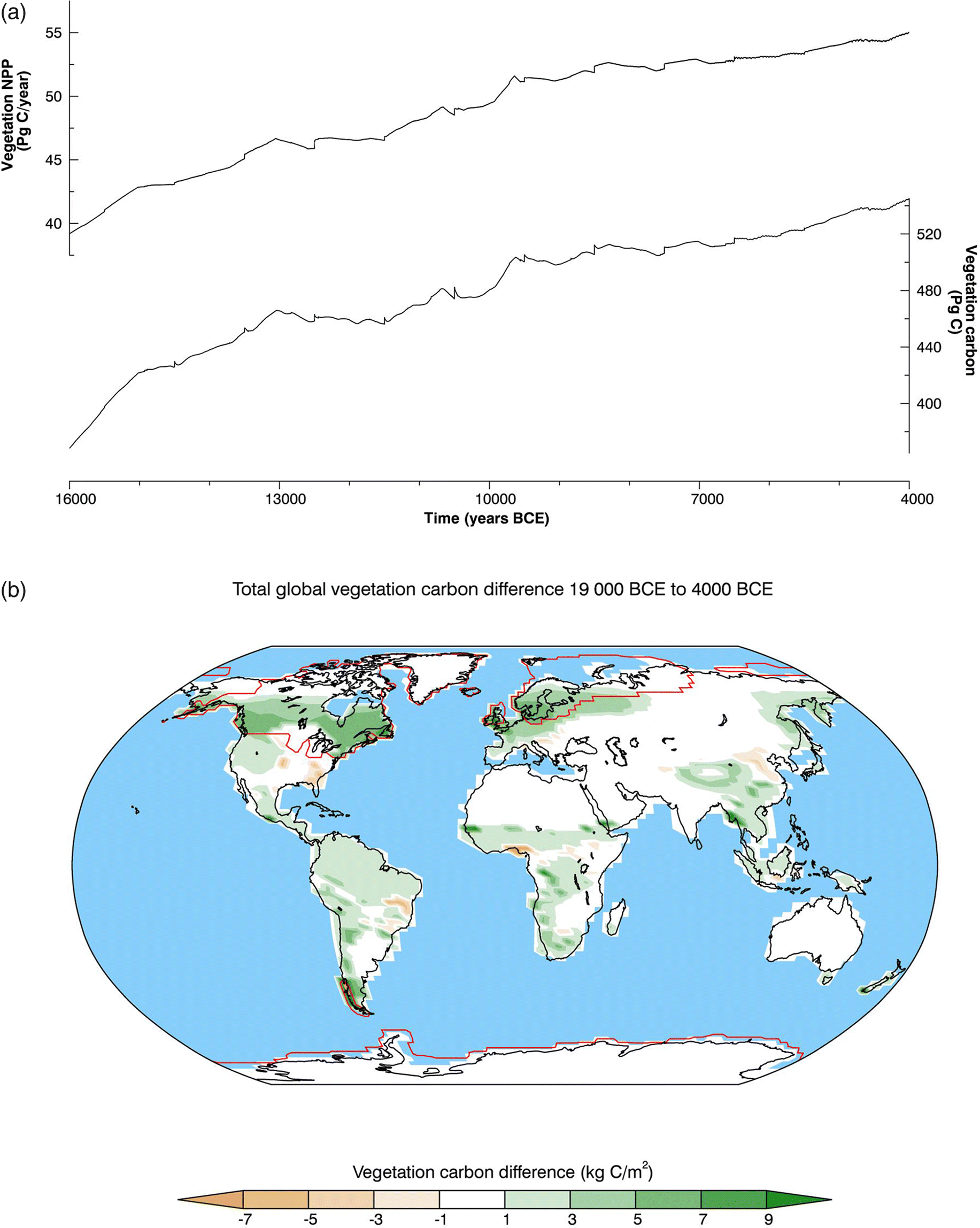
2, ice sheet configuration, and orbital parameters to drive climate change. Our results suggest that alkalinity and DIC fluxes may have increased by as little as 0.063 Pg C/year and 0.024 Pg C/year, respectively, or as much as 0.126 Pg C/year and 0.044 Pg C/year, respectively, between the LGM and the mid-Holocene. The expansion of vegetation following the retreat of continental ice and the resulting rapid increase in vegetation production are the main reasons for the differences in the results among the weathering parameterizations and result from a very different treatment of biological enhancement of weathering by the various model versions. This indicates the importance of obtaining a better understanding of the effect of deglacial vegetation dynamic on the rock cycle.
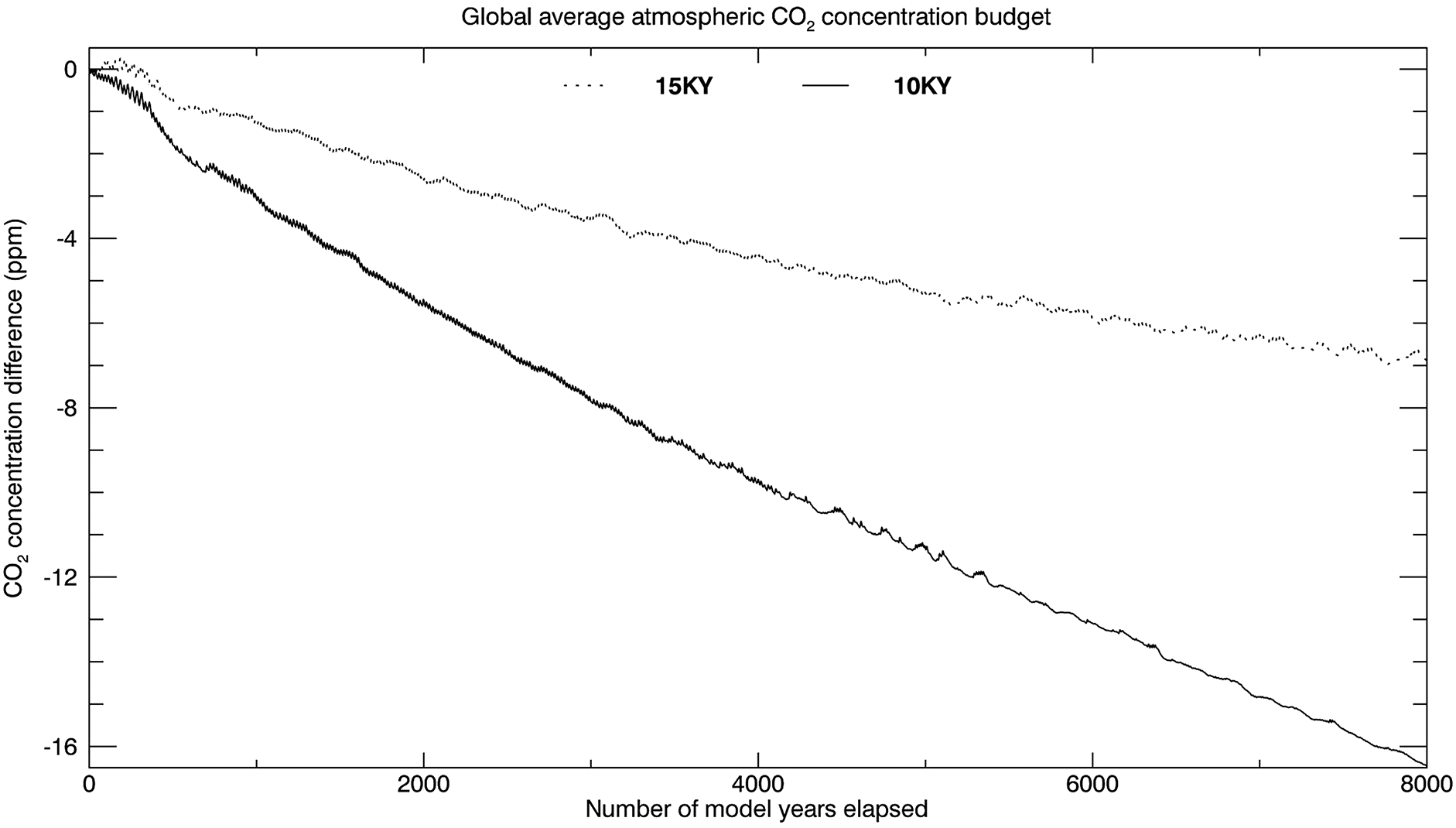
We then prescribed the increases in alkalinity and DIC fluxes obtained from the transient model simulations into the model at specified time points (10 000 BCE and 15 000 BCE) to estimate the effect of these weathering changes on atmospheric CO
2 levels, and to separate the individual contributions of alkalinity and DIC as well as the other external forcings (ice sheet distribution and orbital parameters). We found the impact on atmospheric CO
2 of changes in global weathering fluxes after 8000 model years to be on the order of a 16.5 ppm decrease for 10 000 BCE weathering levels, and about half as much for 15 000 BCE. The individual contributions of alkalinity and DIC were substantial and of opposite direction; where DIC inputs alone led to a net loss of carbon from the ocean to the atmosphere, alkalinity inputs by themselves stimulated a significant CO
2 uptake into the ocean. These two effects combined relatively linearly, resulting in a net increase in ocean carbon (and associated drawdown of atmospheric CO
2) from increased weathering. Based on the different effects of carbonate and silicate weathering on alkalinity and DIC fluxes, these results suggest that the spatial distribution of rock lithology influences the strength of the weathering negative feedback mechanism. This becomes especially important when investigating the effects of land configuration changes, such as would have happened during the deglacial period. Although there are some examples in the literature of rock-type-driven, spatially explicit weathering schemes (
Goddéris et al. 2006;
Taylor et al. 2016), none of these models are incorporated within intermediate-complexity models and thus would be ill-suited to examine changes in weathering on glacial timescales. A two-dimensional weathering model taking into account the worldwide distribution of rock lithology, such as can be found in a recent version of the intermediate-complexity Grid Enabled Integrated Earth System (GENIE) model (
Colbourn et al. 2013), would be better suited for further research in this direction.
This work has demonstrated that global rock weathering rates can be altered in a meaningful way during a period of large climate change such as the latest deglacial period and can result in a nontrivial impact on the global carbon cycle. This box-model study does not take into account the subtleties of two-dimensional rock lithology distribution nor the important geographical changes in weathering distributions inherent to the deglacial period, as would have been induced from ice sheet retreat and sea level change. These are, therefore, important processes to include in further analyses of the effect of deglacial weathering changes on ocean biogeochemistry and climate change.